支持向量机(SVM算法)和软间隔支持向量机概述
日期: 2019-08-10 分类: 个人收藏 499次阅读
支持向量机(SVM算法)和软间隔支持向量机概述
文章目录
(01)决策边界:实现雷区与边界距离最大化(雷区就是边界上的点,找large margin)
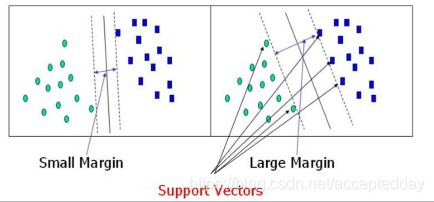
(02)距离的计算:
![[外链图片转存失败(img-hvd3o1Bl-1565427833731)(C:\Users\爱拼才会赢\Desktop\python\支持向量机算法\图片\2.jpg)]](https://img-blog.csdnimg.cn/20190810170423901.jpg?x-oss-process=image/watermark,type_ZmFuZ3poZW5naGVpdGk,shadow_10,text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L2FjY2VwdGVkZGF5,size_16,color_FFFFFF,t_70)
注:
第一步:构造超平面关系式:WTx+b=0得到WT*(x"-x’)=0,即W⊥(x’’-x’)。(W为向量,采用转置便于计算)
第二步:dist(x,h)即为(x-x’)在W的单位方向上映射的模长。
(03)数据标签定义:
Y为样本的类别:
当X为正例的时候Y=+1,当X为负例的时候Y=-1。
引入决策方程:
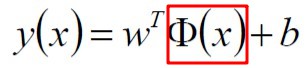 ∮(x)为x的求和变换。
∮(x)为x的求和变换。
然后推导得到yi*y(xi)>0,过程如图:
![[外链图片转存失败(img-tdy1nCr4-1565427833731)(C:\Users\爱拼才会赢\Desktop\python\支持向量机算法\图片\4.jpg)]](https://img-blog.csdnimg.cn/20190810170454567.jpg)
目的:去除 ![[外链图片转存失败(img-dBwfi5Qh-1565427833731)(C:\Users\爱拼才会赢\Desktop\python\支持向量机算法\图片\5.jpg)]](https://img-blog.csdnimg.cn/20190810170507719.jpg) 括号外面的绝对值。
括号外面的绝对值。
得到优化后的distance(x,b,w)距离公式:
![[外链图片转存失败(img-VHzOcwUb-1565427833731)(C:\Users\爱拼才会赢\Desktop\python\支持向量机算法\图片\6.jpg)]](https://img-blog.csdnimg.cn/20190810170516452.jpg)
优化目标:
![[外链图片转存失败(img-kUlS3lPW-1565427833732)(C:\Users\爱拼才会赢\Desktop\python\支持向量机算法\图片\7.jpg)]](https://img-blog.csdnimg.cn/20190810170524750.jpg)
即:使离边界最近的点到边界的距离最大化。
通过放缩,使 ![[外链图片转存失败(img-IRA5qq5f-1565427833732)(C:\Users\爱拼才会赢\Desktop\python\支持向量机算法\图片\8.jpg)]](https://img-blog.csdnimg.cn/20190810170535151.jpg) 的值≧1,所以min(yi(W^T*∮(xi)+b))=1。
的值≧1,所以min(yi(W^T*∮(xi)+b))=1。
最终的目标函数:
内层函数已实现最小化,后面即对![[外链图片转存失败(img-heNn1O31-1565427833732)(C:\Users\爱拼才会赢\Desktop\python\支持向量机算法\图片\10.jpg)]](https://img-blog.csdnimg.cn/20190810170603783.jpg) 进行最大化求解。
进行最大化求解。
(04)目标函数的变换处理:
目标函数max→min转换:
将 ![[外链图片转存失败(img-QF7Zb83a-1565427833732)(C:\Users\爱拼才会赢\Desktop\python\支持向量机算法\图片\11.jpg)]](https://img-blog.csdnimg.cn/20190810170616534.jpg) 转换为
转换为 ![[外链图片转存失败(img-9TnDl7sV-1565427833732)(C:\Users\爱拼才会赢\Desktop\python\支持向量机算法\图片\12.jpg)]](https://img-blog.csdnimg.cn/20190810170628394.jpg) ,
,
且约束条件为: ![[外链图片转存失败(img-53fzH2He-1565427833733)(C:\Users\爱拼才会赢\Desktop\python\支持向量机算法\图片\13.jpg)]](https://img-blog.csdnimg.cn/20190810170637307.jpg) 。
。
采用拉格朗日乘子法求解:
拉格朗日乘子法——不等式约束条件下的求解转换:
![[外链图片转存失败(img-LXV3mvVG-1565427833733)(C:\Users\爱拼才会赢\Desktop\python\支持向量机算法\图片\14.jpg)]](https://img-blog.csdnimg.cn/201908101706470.jpg?x-oss-process=image/watermark,type_ZmFuZ3poZW5naGVpdGk,shadow_10,text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L2FjY2VwdGVkZGF5,size_16,color_FFFFFF,t_70)
对目标函数和约束条件进行整体的变换:
将原约束条件 : ![[外链图片转存失败(img-X8M8rU1t-1565427833733)(C:\Users\爱拼才会赢\Desktop\python\支持向量机算法\图片\15.jpg)]](https://img-blog.csdnimg.cn/20190810170657273.jpg)
转换为 : ![[外链图片转存失败(img-y4xuQF0c-1565427833733)(C:\Users\爱拼才会赢\Desktop\python\支持向量机算法\图片\16.jpg)]](https://img-blog.csdnimg.cn/20190810170705937.jpg)
因此将原式:![[外链图片转存失败(img-mzoIOGsv-1565427833734)(C:\Users\爱拼才会赢\Desktop\python\支持向量机算法\图片\17.jpg)]](https://img-blog.csdnimg.cn/20190810170715859.jpg)
变换为拉格朗日乘子式:
![[外链图片转存失败(img-Yhj8bdOE-1565427833734)(C:\Users\爱拼才会赢\Desktop\python\支持向量机算法\图片\18.jpg)]](https://img-blog.csdnimg.cn/20190810170725607.jpg)
而目标为:
![[外链图片转存失败(img-XZiIJZe9-1565427833734)(C:\Users\爱拼才会赢\Desktop\python\支持向量机算法\图片\21.jpg)]](https://img-blog.csdnimg.cn/20190810170734842.jpg)
(05)SVM求解:
于是根据对偶性质,进行转换:
![[外链图片转存失败(img-jvivsN9Q-1565427833735)(C:\Users\爱拼才会赢\Desktop\python\支持向量机算法\图片\21.jpg)]](https://img-blog.csdnimg.cn/20190810170747141.jpg) 进行转换为
进行转换为![[外链图片转存失败(img-cTk50SLF-1565427833735)(C:\Users\爱拼才会赢\Desktop\python\支持向量机算法\图片\22.jpg)]](https://img-blog.csdnimg.cn/20190810170800367.jpg) 。
。
第一步:对Min L(w,b,α)极小值求解:
然后 ![[外链图片转存失败(img-S9SsrAla-1565427833736)(C:\Users\爱拼才会赢\Desktop\python\支持向量机算法\图片\23.jpg)]](https://img-blog.csdnimg.cn/20190810170826447.jpg) 分别对w,b进行求偏导,求极小值点:
分别对w,b进行求偏导,求极小值点:
![[外链图片转存失败(img-T2l7DZok-1565427833736)(C:\Users\爱拼才会赢\Desktop\python\支持向量机算法\图片\24.jpg)]](https://img-blog.csdnimg.cn/20190810170836561.jpg?x-oss-process=image/watermark,type_ZmFuZ3poZW5naGVpdGk,shadow_10,text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L2FjY2VwdGVkZGF5,size_16,color_FFFFFF,t_70)
并将等式带回 ![[外链图片转存失败(img-puRZseZs-1565427833736)(C:\Users\爱拼才会赢\Desktop\python\支持向量机算法\图片\25.jpg)]](https://img-blog.csdnimg.cn/201908101708504.jpg) 进行进一步化简:
进行进一步化简:
![[外链图片转存失败(img-6UYKyEJQ-1565427833737)(C:\Users\爱拼才会赢\Desktop\python\支持向量机算法\图片\26.jpg)]](https://img-blog.csdnimg.cn/20190810170901768.jpg?x-oss-process=image/watermark,type_ZmFuZ3poZW5naGVpdGk,shadow_10,text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L2FjY2VwdGVkZGF5,size_16,color_FFFFFF,t_70)
当前状态:完成对 ![[外链图片转存失败(img-aGTUqAPu-1565427833738)(C:\Users\爱拼才会赢\Desktop\python\支持向量机算法\图片\25.jpg)]](https://img-blog.csdnimg.cn/20190810170915743.jpg) 的求解工作!
的求解工作!
第二步:对Max L(w,b,α)进行极大值求解:
将 ![[外链图片转存失败(img-m2yF3qWw-1565427833740)(C:\Users\爱拼才会赢\Desktop\python\支持向量机算法\图片\28.jpg)]](https://img-blog.csdnimg.cn/20190810170937849.jpg)
转换为: ![[外链图片转存失败(img-FaqGlIUq-1565427833740)(C:\Users\爱拼才会赢\Desktop\python\支持向量机算法\图片\29.jpg)]](https://img-blog.csdnimg.cn/20190810170949369.jpg)
且 ![[外链图片转存失败(img-YxESSk9T-1565427833740)(C:\Users\爱拼才会赢\Desktop\python\支持向量机算法\图片\30.jpg )]](https://img-blog.csdnimg.cn/2019081017100388.jpg) 。(最终SVM计算式及约束条件)
。(最终SVM计算式及约束条件)
附KTT条件转换解释:
![[外链图片转存失败(img-D0Bpfmbs-1565427833740)(C:\Users\爱拼才会赢\Desktop\python\支持向量机算法\图片\20.jpg)]](https://img-blog.csdnimg.cn/2019081017101414.jpg)
![[外链图片转存失败(img-30q06Qql-1565427833741)(C:\Users\爱拼才会赢\Desktop\python\支持向量机算法\图片\19.jpg)]](https://img-blog.csdnimg.cn/20190810171023992.jpg?x-oss-process=image/watermark,type_ZmFuZ3poZW5naGVpdGk,shadow_10,text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L2FjY2VwdGVkZGF5,size_16,color_FFFFFF,t_70)
(06)SVM实例:
数据为:
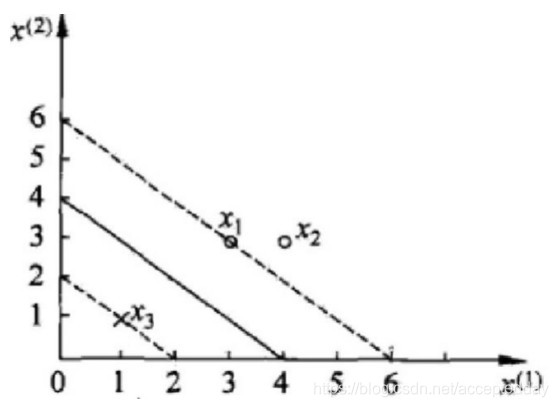
![[外链图片转存失败(img-DNduZu9v-1565427833741)(C:\Users\爱拼才会赢\Desktop\python\支持向量机算法\图片\31.jpg)]](https://img-blog.csdnimg.cn/20190810171035635.jpg)
由约束条件 ![[外链图片转存失败(img-iAdBAQYV-1565427833741)(C:\Users\爱拼才会赢\Desktop\python\支持向量机算法\图片\33.jpg)]](https://img-blog.csdnimg.cn/2019081017104855.jpg) 得到约束条件式为:
得到约束条件式为:![[外链图片转存失败(img-zhDywxPL-1565427833742)(C:\Users\爱拼才会赢\Desktop\python\支持向量机算法\图片\34.jpg)]](https://img-blog.csdnimg.cn/20190810171057747.jpg) ,
,
然后根据 ![[外链图片转存失败(img-Ws2GcY4Y-1565427833742)(C:\Users\爱拼才会赢\Desktop\python\支持向量机算法\图片\35.jpg)]](https://img-blog.csdnimg.cn/20190810171107653.jpg) 对L(α,x,y)进一步计算:
对L(α,x,y)进一步计算:
![[外链图片转存失败(img-8vKG67dk-1565427833742)(C:\Users\爱拼才会赢\Desktop\python\支持向量机算法\图片\36.jpg)]](https://img-blog.csdnimg.cn/20190810171117504.jpg)
结合 ![[外链图片转存失败(img-wSnuYtZY-1565427833742)(C:\Users\爱拼才会赢\Desktop\python\支持向量机算法\图片\37.jpg)]](https://img-blog.csdnimg.cn/20190810171127608.jpg) 进行最终的化简:
进行最终的化简:
![[外链图片转存失败(img-2xUUNC4u-1565427833743)(C:\Users\爱拼才会赢\Desktop\python\支持向量机算法\图片\38.jpg)]](https://img-blog.csdnimg.cn/20190810171138718.jpg) (注:化简式形式不唯一)
(注:化简式形式不唯一)
然后对α1,α2求偏导,得到极小值点:![[外链图片转存失败(img-iHvb3J57-1565427833743)(C:\Users\爱拼才会赢\Desktop\python\支持向量机算法\图片\40.jpg)]](https://img-blog.csdnimg.cn/20190810171150546.jpg) ,但不符合
,但不符合 ![[外链图片转存失败(img-wdm9HRhC-1565427833743)(C:\Users\爱拼才会赢\Desktop\python\支持向量机算法\图片\41.jpg)]](https://img-blog.csdnimg.cn/20190810171201429.jpg) 的条件,舍去结果。
的条件,舍去结果。
根据函数的极值分布特点,所以极值点在边界点(α1=0,或α2=0处):
将α1=0带回原式对α2求极值点得到α2=-2/13(不符合舍去);将α2=0带回原式对α1求极值点得到α1=0.25(符合条件);
于是最终(α1,α2,α3)等于(0.25,0,0.25)。
由 ![[外链图片转存失败(img-cD6uiS5l-1565427833743)(C:\Users\爱拼才会赢\Desktop\python\支持向量机算法\图片\42.jpg)]](https://img-blog.csdnimg.cn/20190810171216786.jpg) 计算w:
计算w:
w=1/4x1x(3,3)+1/4x(-1)x(1,1)=(1/2,1/2)
由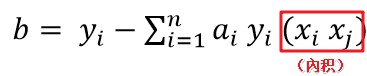 计算b:
计算b:
b=1-(1/4x1x18+1/4x(-1)x6)=-2(这一步计算,我自己也不懂,希望会的评论教我一下。)
最后得到最终的平面方程:
0.5x1+0.5x2-2=0
支持向量:真正发挥作用的数据点,α不为0的点(x1,x3)。
(07)软间隔(soft-margin):
如图:
![[外链图片转存失败(img-Zzinklfq-1565427833744)(C:\Users\爱拼才会赢\Desktop\python\支持向量机算法\图片\48.jpg)]](https://img-blog.csdnimg.cn/20190810171313936.jpg)
注:soft-margin便于边界的泛化,具有一定的松弛度,更为合理。
加入松弛因子:
![[外链图片转存失败(img-GupSGeFu-1565427833744)(C:\Users\爱拼才会赢\Desktop\python\支持向量机算法\图片\44.jpg)]](https://img-blog.csdnimg.cn/20190810171325224.jpg)
新的目标函数:
![[外链图片转存失败(img-E3vzaqDj-1565427833744)(C:\Users\爱拼才会赢\Desktop\python\支持向量机算法\图片\45.jpg)]](https://img-blog.csdnimg.cn/20190810171334772.jpg)
注:当C↑,ξi必须减小,即松弛度降低,对分类准确要求更加严格。
当C↓,ξi可大可小,对分类准确要求更加放松。
新的拉格朗日乘子式:
![[外链图片转存失败(img-WWLfs4GS-1565427833745)(C:\Users\爱拼才会赢\Desktop\python\支持向量机算法\图片\46.jpg)]](https://img-blog.csdnimg.cn/20190810171343583.jpg)
新的最终求解式及约束条件:
![[外链图片转存失败(img-TfIFhrr3-1565427833745)(C:\Users\爱拼才会赢\Desktop\python\支持向量机算法\图片\47.jpg)]](https://img-blog.csdnimg.cn/20190810171351368.jpg?x-oss-process=image/watermark,type_ZmFuZ3poZW5naGVpdGk,shadow_10,text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L2FjY2VwdGVkZGF5,size_16,color_FFFFFF,t_70)
(08)核函数变换:
提升维度-解决低维不可分问题:
![[外链图片转存失败(img-BQ31kwoQ-1565427833745)(C:\Users\爱拼才会赢\Desktop\python\支持向量机算法\图片\49.jpg)]](https://img-blog.csdnimg.cn/20190810171403608.jpg)
应用实例:
![[外链图片转存失败(img-p02Qni7U-1565427833746)(C:\Users\爱拼才会赢\Desktop\python\支持向量机算法\图片\50.jpg)]](https://img-blog.csdnimg.cn/20190810171413171.jpg?x-oss-process=image/watermark,type_ZmFuZ3poZW5naGVpdGk,shadow_10,text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L2FjY2VwdGVkZGF5,size_16,color_FFFFFF,t_70)
附采用高斯函数映射示意图:
![[外链图片转存失败(img-6UbIBmOK-1565427833746)(C:\Users\爱拼才会赢\Desktop\python\支持向量机算法\图片\51.jpg)]](https://img-blog.csdnimg.cn/20190810171421456.jpg?x-oss-process=image/watermark,type_ZmFuZ3poZW5naGVpdGk,shadow_10,text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L2FjY2VwdGVkZGF5,size_16,color_FFFFFF,t_70)
附软间隔向量机详解博客链接:
https://blog.csdn.net/JasonDing1354 除特别声明,本站所有文章均为原创,如需转载请以超级链接形式注明出处:SmartCat's Blog
标签:# 机器学习
上一篇: 简单的E_mail发送
下一篇: JAVA----数组(二)
精华推荐

