时间序列ARIMA模型

平稳性要求:

(1)经由样本时间序列所得到的拟合曲线在未来的一段时间内仍能顺着现有的形态“惯性”地延续下去。

(2)平稳性要求序列的均值和方差不发生明显变化。

严平稳与弱平稳：

严平稳：分布不随时间的改变而改变。如白噪声(正态),期望始终为0，方差为1。

弱平稳：期望与相关系数(依赖性)不变。未来某时刻的t值Xt就要依赖于它的过去信息，所以需要依赖性。

差分法-提升分布的平稳性:

即时间序列在t和t-1时刻的差值。

注：进行一阶差分后分布平稳度增加。

python的实现代码如下：

自回归模型(AR):

描述当前值与历史值之间的关系，用变量自身的历史时间数据对自身进行预测。

自回归模型必须满足平稳性的要求。

p阶自回归过程的公式定义：

μ为常数项，p为阶数，γi为自相关系数，εt为误差。

自回归模型的限制：

(1)用自身数据进行预测。

(2)必须具有平稳性

(3)必须具有自相关性，如果自相关系数(γi)小于0.5，则不宜采用。

(4)自回归只适用于预测与自身前期相关的现象。

移动平均模型(MA)：

关注的是自回归模型中的误差项的累加。

q阶自回归过程的公式定义：

μ为常数项，εt为误差，q为阶数，θ为自相关系数，εt-i为误差项。

移动平均法能有效消除预测中的随机波动。

自回归移动平均模型(ARMA)

自回归模型与移动平均模型的结合。

自回归移动平均模型公式定义：

差分自回归移动平均模型ARIMA(p,d,q):

(全称：Autoregressive Integrated Moving Average Model)

AR是自回归，I是集成，MA为移动平均；p是自回归项，q为移动平均项数，d为时间序列成为平稳时所做的差分次数。

原理：将非平稳时间序列转化为平稳时间序列然后将因变量仅对它的滞后值以及随机误差项的现值和滞后值进行回归所建立的模型。

自相关函数ACF(autocorrelation function):

反映了同一序列在不同时序的取值之间的相关性。

(系数大于0，正相关；小于0，负相关；系数越趋近于0，相关性越低。)

自相关函数公式及范围：

∈

偏相关函数PACF(partial autocorrelation function):

由于自相关函数ACF的自相关系数ρ(k)里掺杂了其他变量对x(t)与x(t-k)的影响，

而偏相关函数PACF是剔除了中间k-1个随机变量x(t-1),x(x-2)…,x(t-k+1)的干扰之后的x(t-k)与x(t)印象的相关程度。

ARIMA(p,d,q)阶数确定：

标准：

​ 截尾：落在置信区间内（95%的点都符合该规则）

通过python的statsmodels库实现自相关函数ACF(autocorrelation function)和相关函数PACF(partial autocorrelation function)的可视化。

关键代码如下：

导库：

ACF和PACF可视化：

​

由图可知ARIMA(p,d,q)=ARIMA(7,1,1)。

模型初步构建完成。

模型评估-AIC与BIC:

模型检验：

在指数平滑模型下，观察ARIMA模型的残差是否是平均值为0且方差为常数的正态分布（服从零均值、方差不变的正态分布），同时也要观察连续残差是否（自）相关。

性质检查-正态分布：

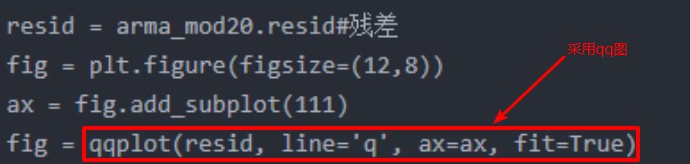
如上图:大部分数据点分布在回归线附近，残差基本符合正态分布。

性质检查-自相关性：

注：如上图的残差相关性较低。（多时间序列点相关性趋近于0，相关性较低。）

关于时间序列AIRMA模型参考博客链接：

    https://blog.csdn.net/u010414589
 除特别声明，本站所有文章均为原创，如需转载请以超级链接形式注明出处：SmartCat's Blog