销售数据：第一列为日期（2015/1/1-2015/2/6），第二列为销售量。

提取链接：https://pan.baidu.com/s/1TR1MvQRS1tt_Q9dXHaTIqg

1.画出时间序列图：

import pandas as pd
import matplotlib.pyplot as plt
import numpy as np

excelFile ='arima_data.xls'
#读取数据，指定日期列为指标，Pandas自动将“日期”列识别为Datetime格式
data = pd.read_excel(excelFile, index_col = u'日期')
data = pd.DataFrame(data,dtype=np.float64)

#时序图
plt.rcParams['font.sans-serif'] = ['SimHei']    #用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False      #用来正常显示负号
data.plot()
plt.show()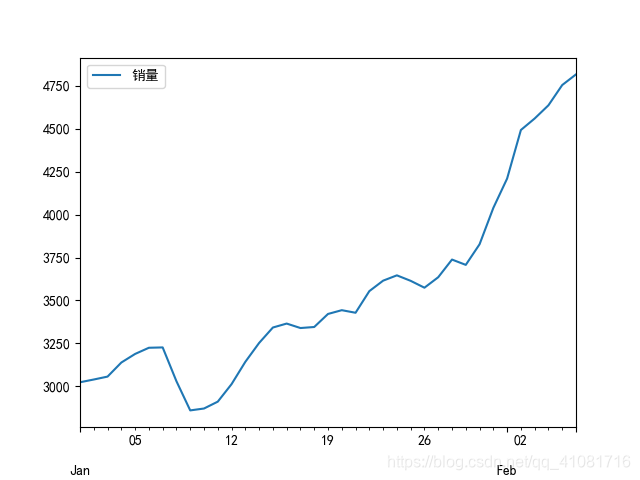

2.判断是否为平稳序列：从时序图可以简单判定是非平稳的，而且用多项式函数也不太好拟合，常见的二次、三次都不可以。（如下自相关是一个三角对称的形式，这种趋势是单调趋势的典型图形）

#自相关图
from statsmodels.graphics.tsaplots import plot_acf
plot_acf(data).show()
plt.show()

同时还可以进行ADF检验： 时间序列的平稳性ADF检验；返回结果为ADF统计量和给定显著性水平下的ADF统计量的临界值；如果ADF统计量比临界值的值小，则可在该显著性水平下，拒绝原序列存在单位根的原假设，即原序列是平稳的 

#平稳性检测
from statsmodels.tsa.stattools import adfuller as ADF
print( ADF(data[u'销量']))
#返回值依次为adf、pvalue、usedlag、nobs、critical values、icbest、regresults、resstore

从运行结果看：ADF值为1.814，大于三个显著性水平条件下的临界值， 所以该序列为一个非平稳序列，

不平稳，怎么办？

3.答案是差分，依次进行1阶、2阶、3阶...差分，直到平稳为止。也就是要对差分后的序列作ADF检验， 分别赋予不同滞后周期，直到ADF值小于三个水平的值为止。

# 差分后的结果
D_data = data.diff().dropna()
D_data.columns = [u'销量差分']

print(D_data)
D_data.plot() #时序图
plt.show()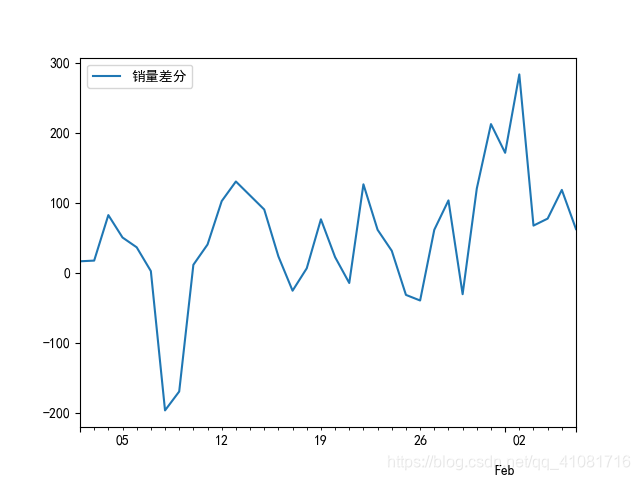

一次差分后，从图像判断基本平稳了 ，然后进行ADF检验，画出自相关图，偏自相关图，得出结果p值为0.01<0.022<0.05，在显著性水平为为0.05下，可以认为差分序列平稳。

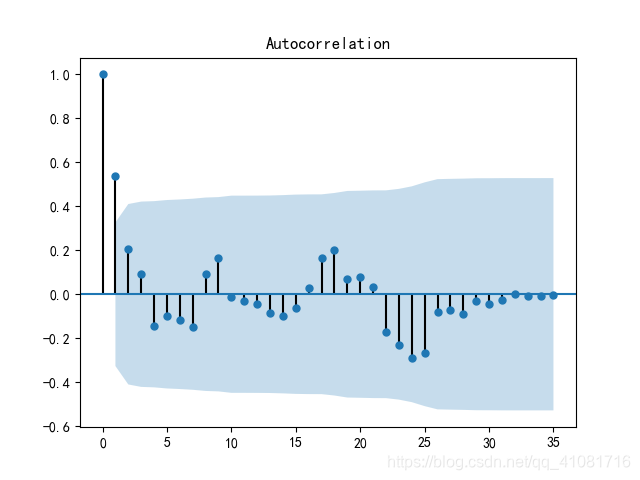
 从ACF图看，截尾；从PACF图看，拖尾，且ACF决定q，PACF决定p，可以尝试选取p=0、1，q=1

除特别声明，本站所有文章均为原创，如需转载请以超级链接形式注明出处：SmartCat's Blog