快速理解机器学习中的偏差与方差

偏差与方差

• 偏差（bias）：偏差度量了学习算法的期望预测与样本真实结果的偏离程度，即刻画了学习算法本身的拟合能力。
• 方差（variance）：方差度量了同样大小的训练集的变动导致的学习性能的变化，即刻画了数据扰动所造成的影响。
• 噪声（noise）：噪声表达了在当前任务上学习算法所能达到的期望泛化误差的下界，即刻画了学习问题本身的难度。

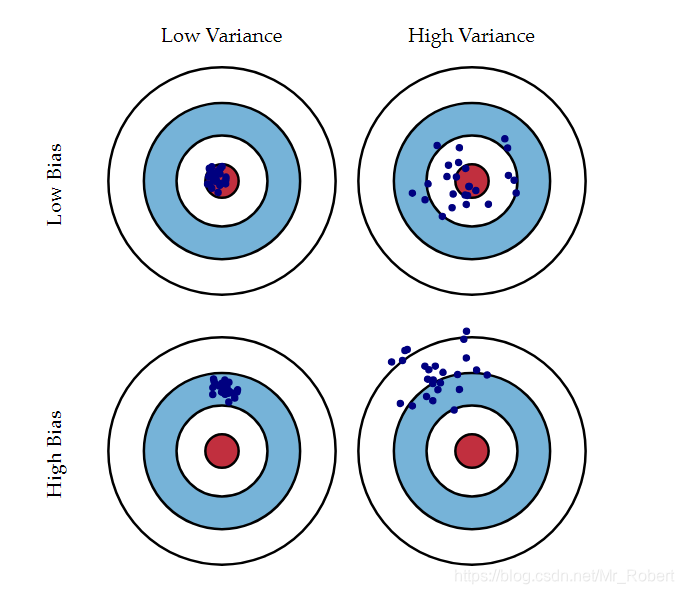
偏差和方差的形象展示如下图所示：（图片引自Understanding the Bias-Variance Tradeoff ）

图中的红色位置就是样本真实值所在的位置，蓝色的点是学习算法每次预测的值。

可以看出，偏差越高，学习算法的预测离真实值越远。而方差越大，学习算法每次预测的值之间波动会比较大。

在模型不断地训练迭代过程中，我们能碰到四种情况：

• 低偏差，低方差：这是训练的理想模型，此时蓝色点集基本落在靶心范围内，且数据离散程度小，基本在靶心范围内；
• 低偏差，高方差：这是机器学习面临的严峻问题：过拟合，也就是模型太贴合训练数据了，导致其泛化（或通用）能力差，若遇到测试集，则准确度下降的厉害；
• 高偏差，低方差：这往往是训练的初始阶段；
• 高偏差，高方差：这是训练最糟糕的情况，准确度差，数据的离散程度也差。

数学定义

符号说明

符号	含义
x	测试样本
D	训练集
yD	x 在数据集中的标记
y	x 的真实标记
f	在训练集D上学得的模型
f(x; D)	训练集D上学得模型f在x上的预测输出

偏差、方差、误差

以回归任务为例，学习算法的期望预测为

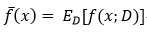
使用样本数相同的不同训练集产生的方差为

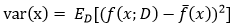
噪声为

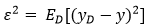
期望输出与真实标记的差别成为偏差，即

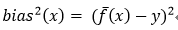
可对算法的期望泛化误差进行分解（公式引自

除特别声明，本站所有文章均为原创，如需转载请以超级链接形式注明出处：SmartCat's Blog