随着深度学习框架的兴起与发展，卷积神经网络的搭建越来越简单。我们可以自行设计网络结构，然后利用深度学习框架，只需要简单的几行代码，就可以搭建好自己的网络模型。虽然模型的搭建很容易，但网络的底层具体是怎么实现的，参数是如何传递的，我们无从可知。本文主要分析了卷积、池化、全连接以及激活函数的反向传播过程（前向传播比较基础，本文不再做分析）以及前向传播、反向传播的python代码实现，整个实现过程完全利用python以及numpy，不借助任何深度学习框架和其他外部代码包。

全连接

全连接的反向传播其实就是BP神经网络的反向传播。反向传播过程主要包括两部分：第一首先根据前一层的梯度确认某一层的梯度，第二根据前一层的梯度计算出W 和 b的梯度。
参考周志华老师的《机器学习》，由链式求导法则，损失函数对某层的梯度等于该层的求导乘以该层与损失函数之间所有层的梯度的累乘。

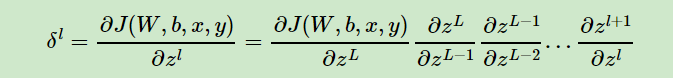
全连接层梯度的更新：

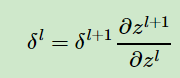
W 和 b 的更新：

代码实现：

	def forward(self,input):
        
        self.input = input
        output = np.dot(self.input, self.w) + self.b
        
        return output
    
    def gra(self,err):
        
        for i in range(err.shape[0]):
            col_input = self.input[i][:, np.newaxis]
            err_i = err[i][:, np.newaxis].T
            self.w_gra += np.dot(col_input, err_i)
            self.b_gra += err_i.reshape(self.b.shape)
        next_err = np.dot(err, self.w.T)
        next_err = np.reshape(next_err, self.input_shape)
        
        return next_err
    
    def backward(self,err,alpha=0.00001,weight_decay=0.0001):
        
        next_err = self.gra(err)
        self.w *= (1 - weight_decay)
        self.b *= (1 - weight_decay)
        self.w -= alpha * self.w_gra
        self.b -= alpha * self.b_gra
        
        self.w_gra = np.zeros(self.w.shape)
        self.b_gra = np.zeros(self.b.shape)
        
        return next_err

卷积

首先，还是简单的介绍一下卷积神经网络的思想。人的大脑在识别图像的过程中，并不是一下子整张图同时识别，而是对于图片中的每一个特征首先局部的感知，然后更高层次对局部综合操作，从而得到全部信息。在图像中，其空间联系也是局部的像素点联系较为紧密，而距离较远的像素相关性则比较弱。因而，每个神经元其实没有必要对全局图像进行感知，只需要对局部进行感知，然后在更高层将局部信息综合起来就得到了全局的信息。这是卷积神经网络具有局部感受野的特点，另一个特点是权值的共享，在整张图片中，所有的局部感受野中的权重是共享的，这大大减少了模型的规模。既然卷积核的权重共享，那么卷积核在一张图的所有局部感受野中只能提取一种特征。解决这个问题的方法是多个卷积核。我们通常用多个不同权重的卷积核对图片进行特征的提取。

对于卷积的反向传播，同样需要两步，第一步确认每一层的梯度误差，第二步确认W 和 b的梯度。
首先，W 和 b的 梯度更新：

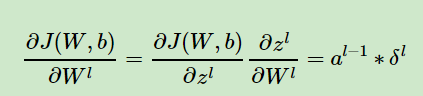
式中a为该层的输入。
由于b只是一个向量，梯度为三维，不能直接相等，通常的做法是子矩阵的项分别求得，得到一个channel维的向量。

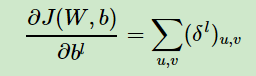
然后是该层梯度的更新。

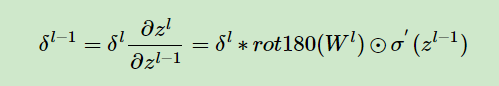
由于卷积的前向传递中，特征中不同的点，与卷积核相乘的次数不同，并且每次相乘的权重不同，所以这里在梯度的更新过程中，对上一层的梯度有补0的操作，对W有翻转的操作，整个梯度的反向传播也利用了卷积操作。这里我是参考了这篇博客。梯度的更新可以结合博客和代码一同理解。

	def forward(self,input):
        
        self.input = input
        col_w = self.w.reshape([-1, self.output_channels])#每一层权重转换为向量
        self.col_image = []
        conv_out = np.zeros(self.output_shape)
        
        for i in range (self.batchsize):
            img_i = self.input[i][np.newaxis, :]#新的轴
            self.col_img_i = img2col(img_i, self.kernal_size, self.stride)
            conv_out[i] = np.reshape(np.dot(self.col_img_i, col_w) + self.b, self.err[0].shape)#eerr[0]是因为这里是单个图片
            self.col_image.append(self.col_img_i)
        self.col_image = np.array(self.col_image)
        
        return conv_out
    
    def gra(self,err):
        
        self.err = err
        col_err = np.reshape(err, [self.batchsize, -1, self.output_channels])
        for i in range(self.batchsize):
            self.w_gra += np.dot(self.col_image[i].T, col_err[i]).reshape(self.w.shape)
        self.b_gra += np.sum(col_err, axis=(0,1))
        
        pad_err = np.pad(self.err,
                      ((0,0),(self.kernal_size-1,self.kernal_size-1), (self.kernal_size-1,self.kernal_size-1), (0,0)),
                      'constant', constant_values=0)
        
        flip_w = np.flipud(np.fliplr(self.w))
        flip_w = flip_w.swapaxes(2,3)
        col_flip_w = flip_w.reshape([-1,self.input_channels])
        col_pad_err = np.array([img2col(pad_err[i][np.newaxis,:], self.kernal_size, self.stride) for i in range (self.batchsize)])
        next_err = np.dot(col_pad_err, col_flip_w)
        next_err = np.reshape(next_err, self.input_shape)
        
        return next_err
    
    
    def backward(self,err,alpha=0.00001,weight_decay=0.0001):
        
        next_err = self.gra(err)
        self.w *= (1 - weight_decay)
        self.bias = (1 - weight_decay)
        self.w -= alpha * self.w_gra
        self.b -= alpha * self.b_gra
        
        self.w_gra = np.zeros(self.w.shape)
        self.b_gra = np.zeros(self.b.shape)
        
        return next_err

	def img2col(img,kernal_size,stride):
    
    img_col = []
    for i in range(0, img.shape[1] - kernal_size+1, stride):
        for j in range(0, img.shape[2] - kernal_size+1, stride):
            col = img[:, i:i+kernal_size, j:j+kernal_size, :].reshape([-1])#每一个感受野大小转换为向量
            img_col.append(col)
    img_col = np.array(img_col)
    
    return img_col

可以看出，整个卷积的前向传播过程，其实是把卷积核和特征层的对应区域做成了向量之间的乘法来处理。

卷积神经网络背后的假设

我们现在知道卷积神经网络大概是怎么回事了，那相比之前的全连接网络的优势体现在什么地方呢？

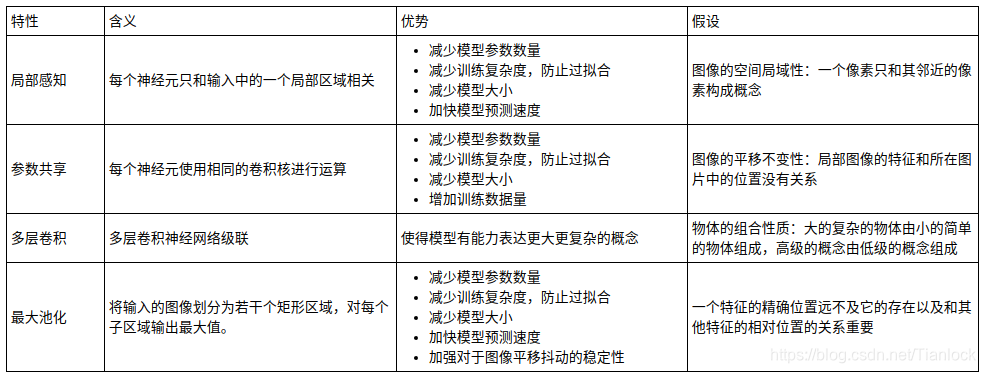
一个特征的精确位置远不及它的存在以及和其他特征的相对位置的关系重要
首先解释一下局部感知，我们从上面的动图可以看出，在卷积层中，每个神经元会对应输入中的一个局部区域(称之为感知域)，其大小是卷积核的尺寸(只考虑单层卷积的时候)，每个神经元的输出只和其对应的感知域有关系，修改感知域外的输入值不会影像该神经元的输出。反过来讲，每个输入节点只会影响感知域包含的神经元。

池化

池化的作用是进行特征的降维，压缩数据和参数量，这可以减小过拟合，同时提高模型的容错性。
另外通常池化有最大池化和平均池化，最大池化一般来说优于平均池化，主要是因为最大是保留主要特征，可以降低平均池化的模糊效应。
池化层没有参数W 和 b，因此，整个反向传播过程主要是池化层梯度的传播。

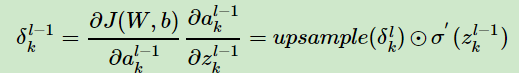
由于池化的前向过程存在降维的操作，所以在池化的反向传播过程中需要上采样，具体操作为把梯度大小首先上采样到池化之前的大小，然后最大池化是对应最大值的位置继承对应位置的梯度，平均池化是整个kernelsize大小的位置为梯度的平均。具体如下图所示。

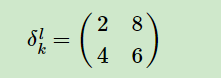
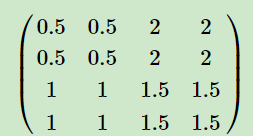
左面为下一层的梯度，右面为最大池化和平均池化的梯度。
代码

	def forward(self,input):
        
        self.input = input
        out = np.zeros([self.input_shape[0], self.input_shape[1] // self.stride, self.input_shape[2] // self.stride, self.output_channels])
        
        for b in range(self.input.shape[0]):
            for c in range(self.output_channels):
                for i in range(0, self.input.shape[1], self.stride):
                    for j in range(0, self.input.shape[2], self.stride):
                        out[b, i // self.stride, j // self.stride, c] = np.max(self.input[b, i:i + self.kernal_size, j:j + self.kernal_size, c])
                        index = np.argmax(self.input[b, i:i + self.kernal_size, j:j + self.kernal_size, c])
                        self.index[b, i + index // self.stride, j + index % self.stride, c] = 1
                        
        return out
    
    def backward(self,err):
        
        err = np.reshape(err, self.output_shape)
        
        return np.repeat(np.repeat(err, self.stride, axis = 1), self.stride, axis = 2) * self.index

激活函数

激活层相当于对网络进行一次非线性映射，如果不采用激活函数，那么每一层的输出都是输入的线性函数，无论多少神经网络层，输出都是输入的线性组合，与没有隐含层的效果是一样的。
sigmoid：

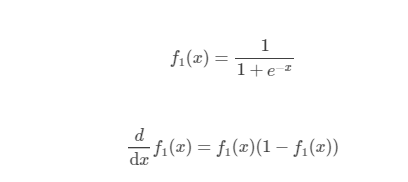
ReLU：

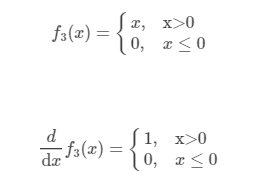
代码：ReLU

	def forward(self,input):
        
        self.input = input
        
        return np.maximum(self.input, 0)
    
    def backward(self,err):
        
        self.err = err
        self.err[self.input < 0] = 0
        
        return self.err

Softmax代码：

    def calculate_loss(self,prediction,label):
        
        self.predict(prediction)
        self.label = label
        self.loss = 0
        for i in range(self.batchsize):
            self.loss += np.log(np.sum(np.exp(prediction[i]))) - prediction[i,label[i]]
            
        return (self.loss / self.batchsize)[0]
    
    def backward(self):
        
        self.err = self.softmax.copy()
        for i in range (self.batchsize):
            self.err[i, self.label[i]] -= 1
            
        return self.err

本文回顾了自行构建卷积神经网络的主要模块，整个逻辑比较乱（我在写的时候就感觉出来了），其实整个流程是我之前用np实现mnist手写数据集的一个工程，我把核心的代码都搬到这里来了。如果有错误的地方还请大佬们指正。
文章的公式图片来自于刘建平老师的博客。
参考资料：
1，DNN反向传播，CNN反向传播
2，《机器学习》，周志华
3，Deep Learning, book by Ian Goodfellow, Yoshua Bengio, and Aaron Courville