“具体情况具体分析”是马克思主义活的灵魂。

上一节我们讨论了直方图的均衡化，本来以为万千世界归一了。可事实无情的打脸，简单的说，直方图均衡化不能解决一切问题。

一般来说，直方图均衡能够自动地确定变换函数，且输出结果比较好，当时需要自动增强时是一种好方法。但有的情况下，使用直方图均衡并不是最好的办法。有时候我们可以指定特定的直方图，而不是均匀分布的直方图，并让原图像的直方图变换成我们指定的形式。这个过程称为直方图匹配或者直方图规定化。

直方图均衡能不能搞定一切？一个例子引发的血案。

我们先回想一下直方图均衡的初衷是什么：直方图均衡化处理的“中心思想”是把原始图像的灰度直方图从比较集中的某个灰度区间变成在全部灰度范围内的均匀分布。直方图均衡化就是对图像进行非线性拉伸，重新分配图像像素值，使一定灰度范围内的像素数量大致相同。

关键词就是均匀分布和非线性拉伸。

我们来看一张图：

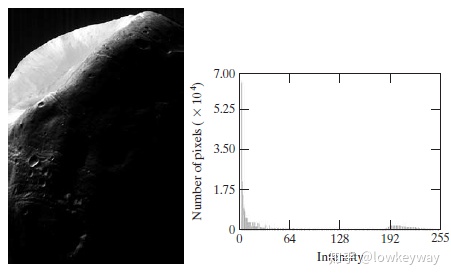
这是一张NASA的火星表面探测器拍摄的火星图片，肉眼看就是比较暗，对比度低。我们转换成直方图表示就可以证明这一点，大部分的像素都分布在接近于0的低灰度级周边。根据我们上一章讲的直方图均衡的作用和其典型的应用不就是低对比度变成高对比度吗？

来吧，我们做一次直方图均衡变换：

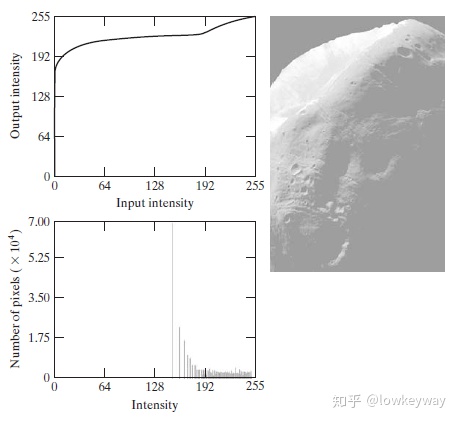
怎么会这样？虽然图片确实变亮了，但是对比度没有明显增加啊！而且直方图为什么不是我们期望的均值分布呢？

查漏补缺，找出原因。

要想找出产生这种现象的原因，我们可能需要倒回上一章。发现一个容易被忽略的细节上，连续和离散的区别。

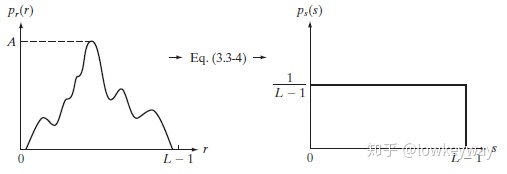
我们推导均值变换函数

连续函数中任何一小段函数图像都可以被拆分成无数个点，但是离散函数很可能会在点与点中的间隔中丢失掉一些特性，如果我们够细心，应该对下面这张图有过疑问：

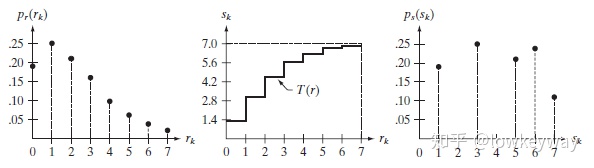
虽然变换后的

造成这个现象的根本原因就是离散函数是对连续函数的采样和和量化，采样频率的大小决定了细节丢失的程度。所以离散的直方图知识PDF的一个近似，而且处理过程中还不允许造成新的灰度级，所以在实际的直方图应用中很少看到完美平坦的直方图。它只能代表了一种趋势，比如做到了变换后的灰度级跨越了更宽的灰度级范围，最终达到了增大对比度的目的。

对数字图像的直方图均衡补充了这一段之后，瞬间感觉对直方图均衡的崇拜下降了一个等级。知道了离散函数的这个特点，就容易理解为什么这个例子中的直方图均衡后为什么没有做到完美的均值分布了。

不气不馁，寻找解决方案

如果我们看到这里就扫兴得叹气回家，感叹世态炎凉。这怎么会是咱们做工程研发人的心态？直面问题，解决问题。

我们再来针对这单个问题定量分析一下，主要问题点在哪里。我们把

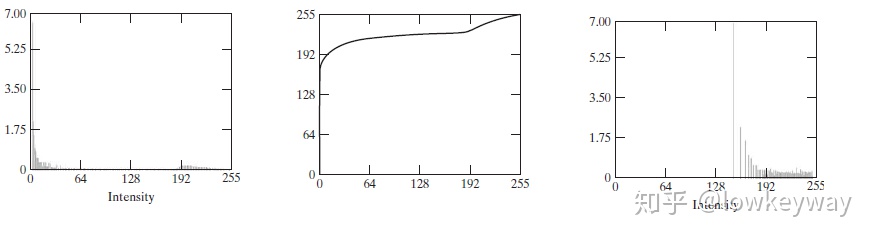
我们看到变换函数

好，如果原因是这个，怎么解决呢？

老规矩：大胆假设，小心求证

我们想，如果有一个跟

由上图可以看出，我们只是对原始图像做了一点变化，即把它对应的归一化的直方图（密度函数）靠近0的这些值向大的方向偏移了一点点。就得到了对比度更高的结果。找到解决方案，打完收工。

这个方法不错，要是我们能够推广一下，对于任意一个输入

你只管提问题，我来帮你解决。

雷神说：这不是没有可能。

如果说引入这个问题的根本原因是连续函数和离散函数的特性导致的。那么解铃还须系铃人。我们再退回连续密度函数。

先明确一下目的，以免在繁杂的数学公式变换中迷失了自我。

• 对于一个给定的输入图像估计
  ,我们是想要找到这么一个我们期望（指定）的概率密度函数
  它可以在变换后有着跟给定输入图像相同的特征。

首先，我们已经知道了 的变换：

那么，我们要找对应的随机变量

把两个等式合并，就可以求得z：

就这样，搞定了？先别管对不对，总结一下路径：

1. 由图像得到
   ，并由对应的
   计算出来
2. 这个
   就是我们对
   做
3. 求反变换

总结一下：先对输入图像做均值变换，然后对均值变换后的图像做

哈哈，三两个公式就搞定了？总感觉哪里怪怪的。

理一下，已知条件就两个：

• 一张图
• 一个目标灰度的PDF（
  ）

就可以得到我们期望的概率分布函数

看似简单，但是这里面有一些隐含条件非常重要：

• 一张图

我们就已知了原始

• 一个目标灰度的PDF（
  ）

我们知道，一张图的直方图均衡化后的

直方图匹配原来就是一个求一次直方图均值再做一次反变换。

忘了补充，只要把这个思路再拓展到离散域就可以啦。