卷积神经网络基础：

首先看一下全连接网络，即神经元和相邻层上的每个神经元都连接：

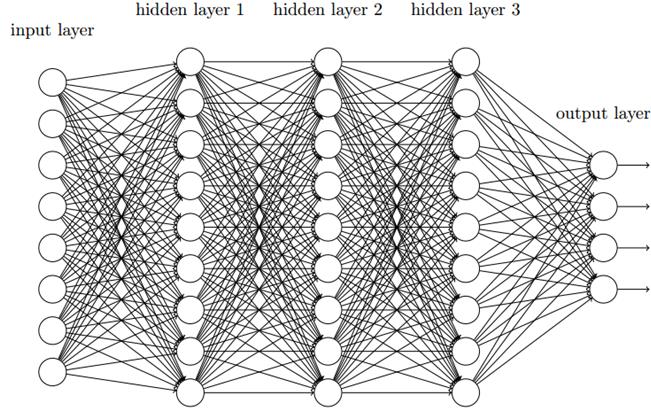
如果我们把图像中的像素点顺序排列作为输入层神经元的值，对于28x28像素的图像，输入神经元有28x28=784个。但是用这种全连接的网络去做图像分类是很奇怪的，因为它没有考虑图像的空间结构（局部特征），它相同看待那些相距很近和很远的像素，这是不好的。

卷积神经网络三个重要概念：

1. 局部感受野（local receptive fields）
2. 共享权重（shared weights）
3. 池化（pooling）

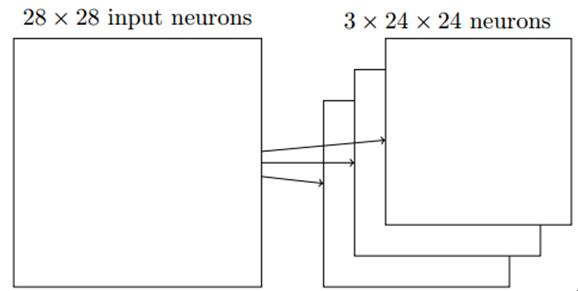
（1）局部感受野：在全连接的网络中，输入被描绘成纵向排列的神经元，但是在卷积网络中我们把它看成28x28的方形：

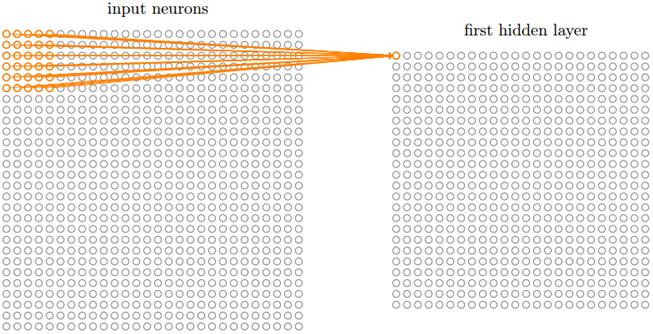
输入神经元的一小片区域会被连接到下一层隐层，这个区域被称为局部感受野，然后在输入图像中移动局部感受野，每移动一次，对应一个隐层的神经元，如此重复构成隐层所有神经元。如果局部感受野是5x5的，一次移动一格，输入图像是28x28的，那么隐层有24x24个神经元。

（2）共享权重和偏置：每个隐层的神经元都有一个偏置和连接到它的局部感受野的5x5的权重，并且对这一层的所有神经元使用相同的权重和偏置。也就是说，对于隐藏层的第j行第k列的神经元，它的输出为：

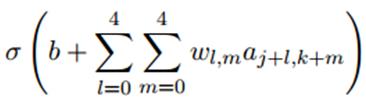
其中σ是激活函数，b是共享偏置，Wl,m是共享权重的5x5数组，用ax,y表示输入层的第x行第y列的神经元的输出值，即隐层的第j行第k列的神经元的若干个输入。

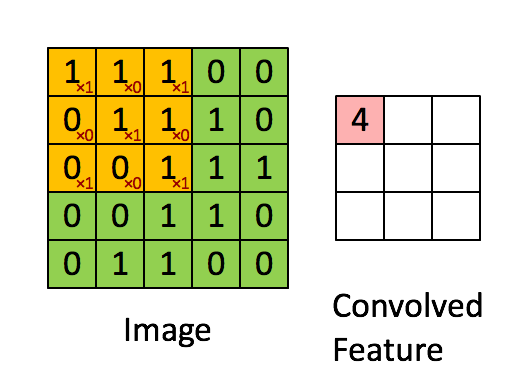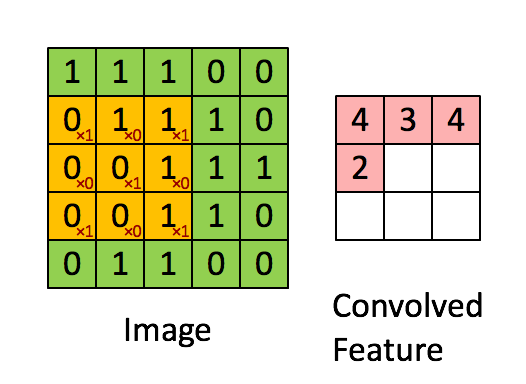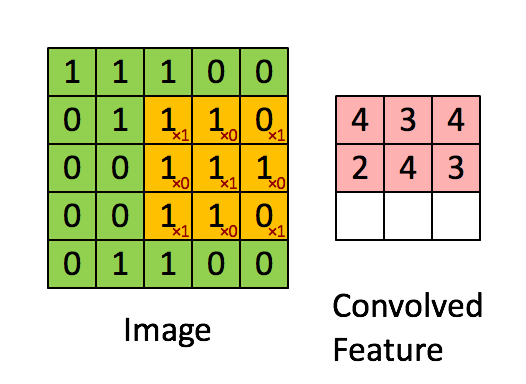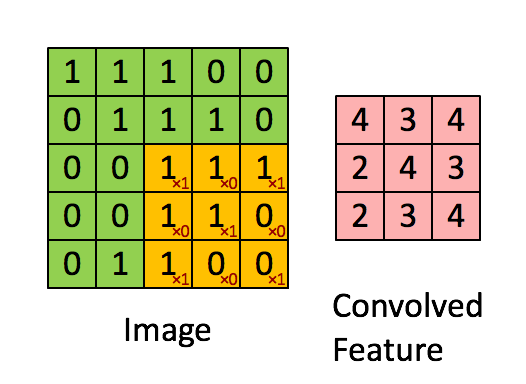
共享，意味着这一个隐层的所有神经元检测完全相同的特征，在输入图像的不同位置。这说明卷积网络可以很好地适应图片的平移不变性。共享权重和偏置被称为卷积核或者滤波器。我们再看一下卷积的过程：

图像分类中我们会卷积多次（卷积核不同），也称为特征映射，下图卷积了3次，识别了3种特征：

共享权重和偏置的一个很大的优点是，大大减少了网络的参数数量。一次卷积我们需要5x5=25个共享权重，加上一个共享偏置共26个参数。如果我们卷积了20次，那么共有20x26=520个参数。以全连接对比，输入神经元有28x28=784个，隐层神经元设为30个，共有784x30个权重，加上30个偏置，共有23550个参数。卷积层的平移不变性会减少参数数量并加快训练，有助于建立深度网络。

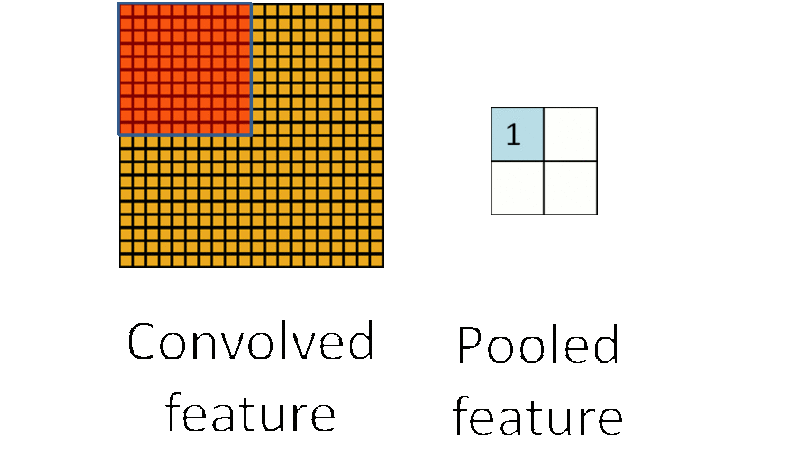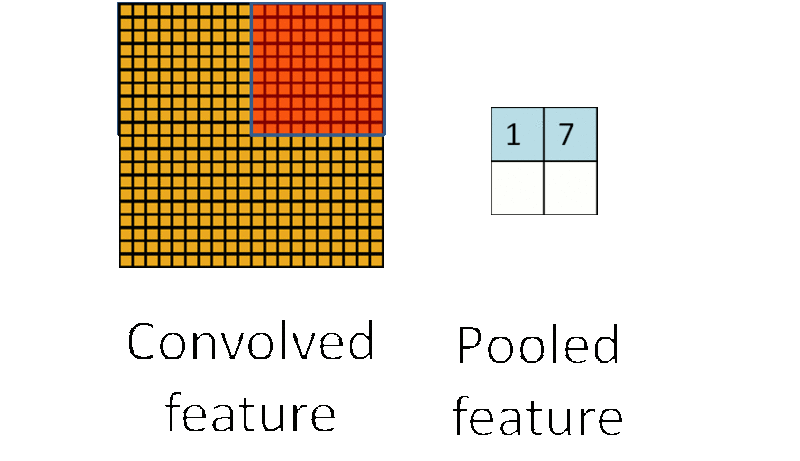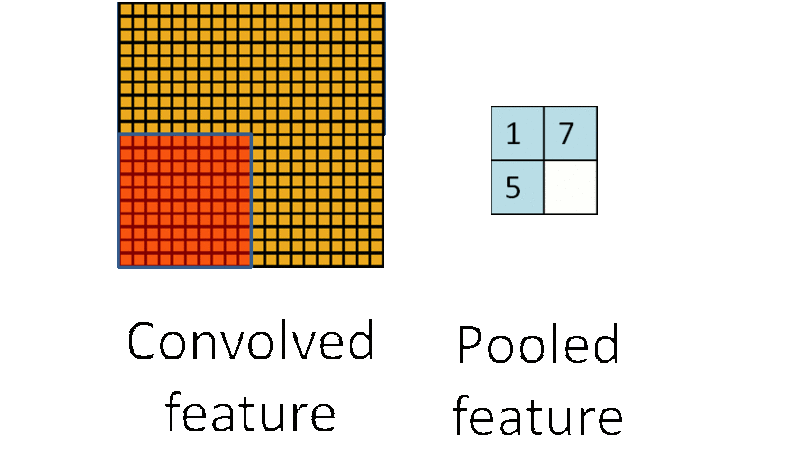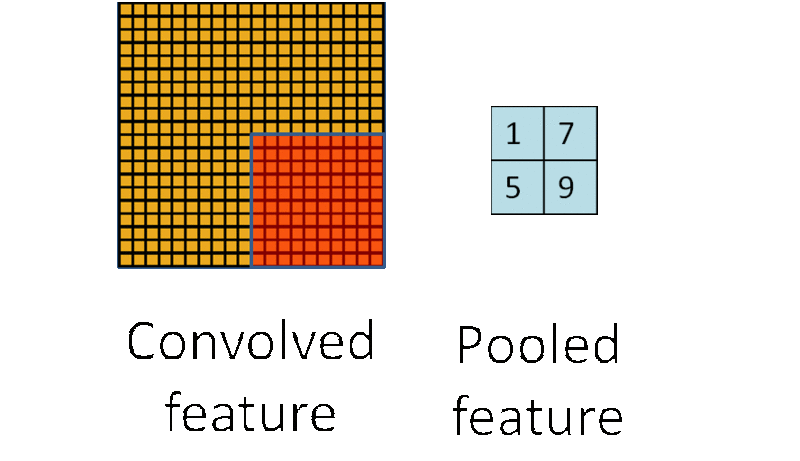
（3）池化：池化层一般在卷积层之后使用，主要是简化从卷积层输出的信息。池化层的每个单元概括了前一层的一个小区域，常见的方法有最大池化，它取前一层那个小区域里的最大值作为对应池化层的值。

为什么要池化呢？在通过卷积获得了特征之后，下一步我们要利用这些特征去做分类，如果直接用这些特征去训练分类器，维度还是太高，计算量太大而且容易过拟合，而通过池化大大减少特征的维度，减少过拟合的出现。再者，我们选择图像中的连续范围作为池化区域，这就意味着即使图像经历了一个小的平移之后，依然会产生相同的 (池化的) 特征，做到了图片的平移不变性。这里也可以看到卷积池化共享权重都有类似的作用。

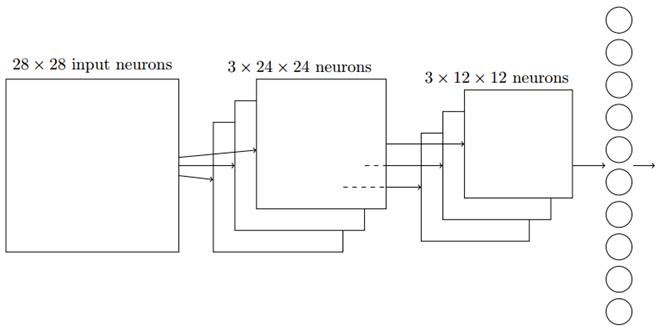
最后要知道，卷积层往往不止一个特征映射，多层卷积的目的是一层卷积学到的特征往往是局部的，层数越高，学到的特征就越全局化。所以我们也将最大池化分别应用于每一个特征映射，如下图，最后是一个输出层，和池化层全连接，一个神经元代表一个类别：

需要注意的是，以上我们举的例子都是单通道的图像，实际上我们的输入图像一般是三通道的，也就是说是一个三维的张量，而对应的卷积核也是三维的，卷积核的“厚度”和输入图像的“厚度”是相同的，三通道就意味着“厚度”为3，所以这个卷积核也是三层。接下来计算第一个通道和卷积核对应第一层的卷积，同样的，计算第二、三个通道和卷积核对应第二、三层的卷积，卷积就是矩阵对应元素相乘之后再相加。最后这三个结果相加，在加上偏置，作为输出。如下图：

如果再多一个卷积核，就再重复一次上边的运算，最后的输出加一层，“厚度”变为2。

卷积神经网络的反向传播：

首先回顾一下一般的前馈神经网络的反向传播：

详细内容可参看：

除特别声明，本站所有文章均为原创，如需转载请以超级链接形式注明出处：SmartCat's Blog