【python】拉格朗日插值法 和 牛顿插值法
日期: 2020-06-17 分类: 个人收藏 563次阅读
0.前言
0.1 摘要
本文主要讲解了拉格朗日插值法和牛顿插值之间的对比。对于具体插值原理不做深入探讨,如有需要看参考文后的参考文献。
0.2 插值、拟合、逼近的几点说明[4]
- 插值:已知若干离散的点,根据这若干离散的点,推断出经过这些离散点的函数或求出这些之间的函数值
- 拟合:根据若干离散的数据,希望得到一个连续的函数,或是更加密集的离散方程与已知点相吻合,这个过程叫做拟合。
- 最小二乘意义下的拟合,是要求拟合函数与原始数据均方误差达到最小,不需要经过这些点,或是说不需要完全经过这些点。
1.正文
1.1 拉个朗日插值法
1.1.1 程序
#!/usr/bin/env python
# -*- coding: utf-8 -*-
import numpy as np
import matplotlib.pyplot as plt
import time
#print(plt.__file__ )
def lagrange(X, Y, xx):
"""拉格朗日插值法"""
result = 0.0
for i in range(len(Y)):
f_temp = Y[i]
for j in range(len(Y)):
if i != j:
f_temp *= (xx - X[j]) / (X[i] - X[j])
result += f_temp
return result
def plot_image(X, Y, xq, yq,num):
# 绘图
plt.title("Lagrange_interpolation") # 打印标题
plt.plot(X, Y, 's', label="original values") # 蓝色点表示原来的值
plt.plot(xq, yq, 'r', label="interpolation values") # 插值曲线
words = "被插点数:{}".format(num)
plt.text(3.5,-10,words,fontproperties='SimHei')
plt.xlabel('x')
plt.ylabel('y')
plt.legend(loc=4) # 指定lgend的位置
plt.savefig('lagrange.png')
plt.show()
def main():
# 开始计时
start_time = time.clock()
# 已30
X = [-1, 0, 1, 2, 3, 4, 5]
Y = [-20, -12, 1, 15, 4, 21, 41]
# 计算的插值点
num = 50 # 被插点数
xq = np.linspace(np.min(X), np.max(X), num, endpoint=True)
yq = []
for xx in xq:
yq.append(lagrange(X, Y, xx))
# 绘图
plot_image(X, Y, xq, yq,num)
# 结束计时
end_time = time.clock()
consumer_time = end_time - start_time
print("程序运行消耗时间: " + str(consumer_time))
if __name__ == '__main__':
main()
1.1.2 运行结果
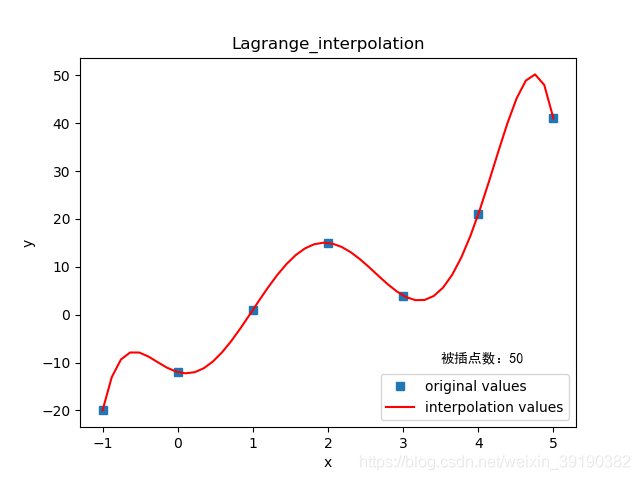
---------------------------------------------------图1 拟合效果图
-------------------------------------------------图2 程序运行时间
1.2 牛顿插值法
1.2.1 程序
#!/usr/bin/env python
# -*- coding: utf-8 -*-
import matplotlib.pyplot as plt
from pylab import mpl
import numpy as np
import pandas as pd
import math
import time
# %matplotlib inline
def get_diff_table(X, Y):
""" 得到差商表"""
n = len(X)
A = np.zeros([n, n])
for i in range(0, n):
A[i][0] = Y[i] # 零阶均差
for j in range(1, n):
for i in range(j, n):
A[i][j] = (A[i][j - 1] - A[i - 1][j - 1]) / (X[i] - X[i - j])
return A
def newton_interpolation(X, Y, xx):
""" 计算x点的插值
1. f(x) = f(x0) + f[x0,x1](x-x0)+…… 牛顿插值函数
2. f[x0,x1] = (f(x0)-f(x1))/(x0-x1) chashang 差商
3. (x-x0)(x-x1)…… x_diff 牛顿插值中,和差商相乘的那一项
"""
fx = Y[0] # f(x0)
chashang = np.zeros((len(X), len(X))) # 差商表
x_diff = 1.0
# 将第0列赋值
for j in range(0, len(X)):
chashang[j, 0] = Y[j] # 零阶差商 第零列差商
# 计算插值
for j in range(1, len(X)): # 列
# 计算x的多项式 x_diff
x_diff = x_diff * (xx - X[j - 1])
# 从第1列到第n列计算差商
for i in range(j, len(X)): # 行
chashang[i, j] = (chashang[i, j - 1] - chashang[i - 1, j - 1]) / (X[i] - X[i - j])
fx = fx + x_diff * chashang[j, j]
return fx
def plot_image(X, Y, xq, yq,num):
# 绘图
plt.title("Newton_interpolation") # 打印标题
plt.plot(X, Y, 's', label="original values") # 蓝色点表示原来的值
plt.plot(xq, yq, 'r', label="interpolation values") # 插值曲线
words = "被插点数:{}".format(num)
plt.text(3.5,-10,words,fontproperties='SimHei')
plt.xlabel('x')
plt.ylabel('y')
plt.legend(loc=4) # 指定lgend的位置
plt.savefig('niudun.png')
plt.show()
def main():
# 计算时间
start_time = time.clock()
# 已知点
X = [-1, 0, 1, 2, 3, 4, 5]
Y = [-20, -12, 1, 15, 4, 21, 41]
# 计算的插值点
num = 50 # 被插点数
xq = np.linspace(np.min(X), np.max(X), num, endpoint=True)
yq = []
for xx in xq:
yq.append(newton_interpolation(X, Y, xx))
# 绘图
plot_image(X, Y, xq, yq,num)
# 结束计算时间
end_time = time.clock()
consumer_time = end_time - start_time
print("程序运行消耗时间: " + str(consumer_time))
if __name__ == '__main__':
main()
1.2.2 结果
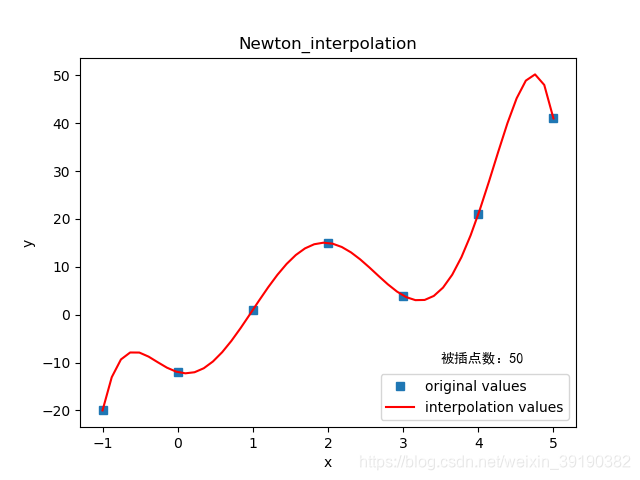
---------------------------------------------------图1 拟合效果图

-------------------------------------------------图2 程序运行时间
1.3. 讨论
- 拉格朗日插值法结构紧凑,形式优美,但在实际计算中,当插值点增加或减少时,多项式需要全部重新计算,非常不经济。
- 对于等距基点且插值节点多的情况会出现龙格(Runge)现象
- 由于差商表的建立,当增加或减少新节点时,只需要计算部分,牛顿插值具有承袭性。
参考文献
[1] https://blog.csdn.net/shenwansangz
除特别声明,本站所有文章均为原创,如需转载请以超级链接形式注明出处:SmartCat's Blog
标签:插值
上一篇: 泡着枸杞写bug的三流程序员凭什么逆袭到一线大厂?
下一篇: (十四)Django学习——Auth系统中的表,auth系统中的User模型使用,使用auth系统实现注册登录案例;使用auth系统进行指定视图的四种权限的设置,给指定用户添加权限,给组添加权限!
精华推荐

