Slides：百度云 提取码: gs3n

优化

优化的本质目标就是
$${\omega }^{\ast }=argmi{n}_{\omega }L(\omega )$$
其中的$L(\omega )$是Lost函数，即，找到能够使得$L(\omega )$最小的$\omega$。

优化的方式

随机搜索（愚蠢的决定）

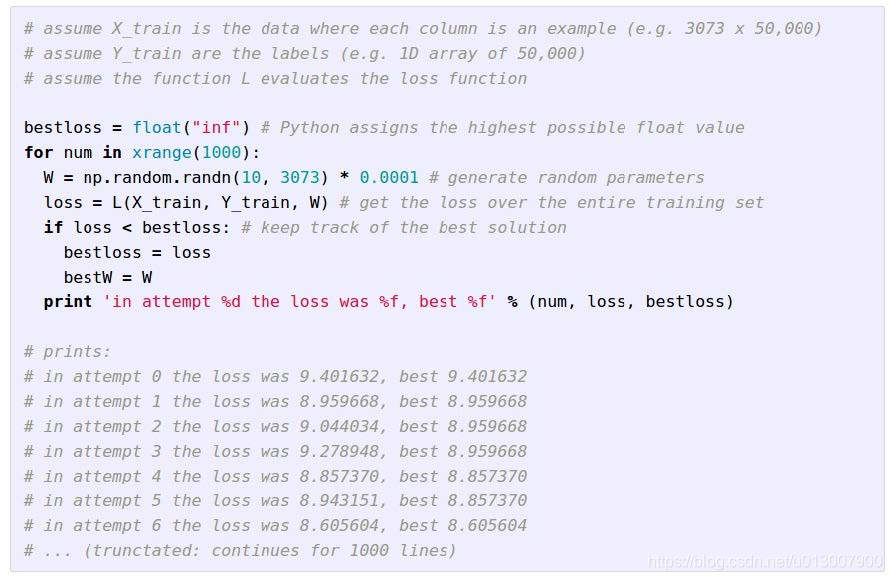
梯度计算

对于一维函数，通过微分得到梯度
$$\frac{df(x)}{dx}=\underset{h\to 0}{\lim }\frac{f(x+h)-f(x)}{h}$$
对于多维函数，梯度则是一个由各维度的偏微分组成的向量。

沿着梯度的反方向前进就能得到最速下降的方向。

数值渐变

对于每一个维度，取一个较小的$h$；然后模拟微分的过程来计算

比较慢，主要用于参照和debug

分析渐变

用Loss函数的微分公式直接计算

$$\begin{gathered} L=\frac{1}{N}\sum _{i=1}^N{L}_i+\sum _k{W}_k^2 \\ Li=\sum _{j\ne y_j}max(0,s_j-s_{y_j}+1) \\ \Rightarrow {\nabla }_{W}L \end{gathered}$$

有的时候，不知道如何debug，可以用数值渐变来进行一个验证。

Pytorch doc
torch.autograd.gradcheck(func: Callable[…, Union[torch.Tensor, Sequence[torch.Tensor]]], inputs: Union[torch.Tensor, Sequence[torch.Tensor]], eps: float = 1e-06, atol: float = 1e-05, rtol: float = 0.001, raise_exception: bool = True, check_sparse_nnz: bool = False, nondet_tol: float = 0.0, check_undefined_grad: bool = True) → bool

梯度下降

w = initalize_weights()
for t in range(num_steps):
    dw = compute_gradient(loss_fn, data, w)
    w -= learning_rate * dw

超参数：

• 权重初始化
• 步骤数
• 学习率

随机梯度下降（SGD）

我们计算一个全训练集的梯度时，往往比较费时费力；那么我们就随机选出一些批次（minibatch）的数据，类似一组有32/64/128个，计算他们的梯度，这样就更加轻松。

$$\begin{gathered} L=\frac{1}{N}\sum _{i=1}^N{L}_i+\sum _k{W}_k^2 \\ {\nabla }_{w}L(W)=\frac{1}{N}\sum _{i=1}^N{\nabla }_w{L}_i(x_i,y_i,W)+\lambda {\nabla }_{w}R(W) \end{gathered}$$

w = initalize_weights()
for t in range(num_steps):
	minibatch = sample_data(data, batch_size)
    dw = compute_gradient(loss_fn, minibatch, w)
    w -= learning_rate * dw

超参数：

• 重量初始化
• 步骤数
• 学习率
• 批量
• 数据采样

通过多次随机抽样来获得近似的梯度方向。

可视化demo

SGD的问题

如果损失在一个方向上快速变化而在另一个方向上缓慢变化怎么办？
梯度下降会怎么变化？
梯度下降的方向会反复横跳，导致效率低下

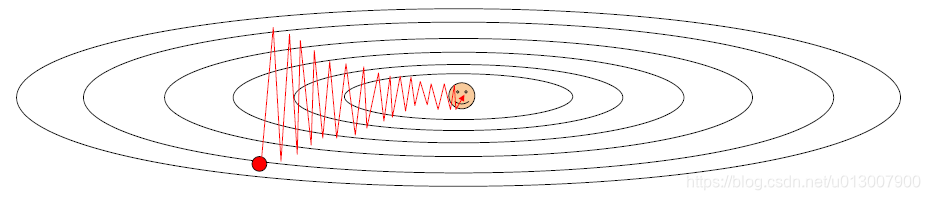
Loss函数的condition number：Hessian矩阵的最大与最小奇异值之比大

区域最小值与鞍点

在区域最小值与鞍点，会有零梯度，梯度下降被卡住

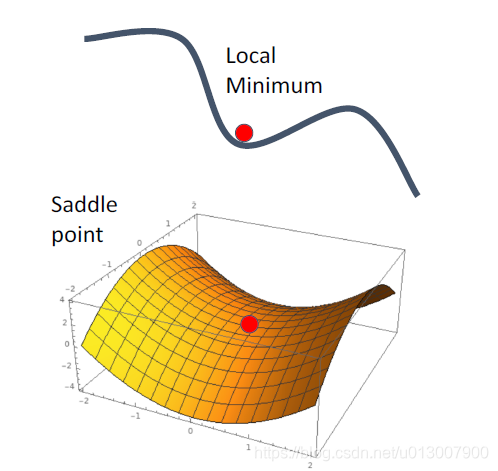
随机梯度下降 + 动量（SGD+Momentum）

动量就是之前SGD方向的累计影响
也正是因为有累积影响，导致梯度下降的时候容易过度跑偏

Nesterov Momentum

原本的动量更新方式：
在现有的点，同时计算梯度下降方向与动量方向

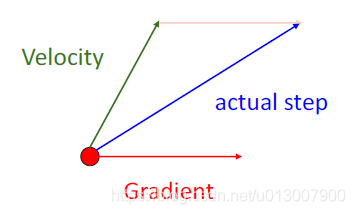
Nesterov动量：
先迭代一次动量，再在新的位置重新计算梯度

$$\begin{gathered} v_{t+1}=\rho v_t-\alpha \nabla f(x_t+\rho v_t) \\ {x}_{t+1}=x_t+v_{t+1} \end{gathered}$$

适应性随机梯度下降

w = initalize_weights()
grad_squared = 0
for t in range(num_steps):
    dw = compute_gradient(w)
    grad_squared += dw * dw
    w -= learning_rate * dw / (grad_squared.sqrt() + 1e-7)

沿“陡峭”方向的前进受到抑制；沿“平坦”方向的进展加快

但是因为grad_squared是有累加的，从而会导致到后期增量可能被抑制得太过了

RMSProp

w = initalize_weights()
grad_squared = 0
for t in range(num_steps):
    dw = compute_gradient(w)
    grad_squared = decay_rate * grad_squared + (1 - decay_rate ) * dw * dw
    w -= learning_rate * dw / (grad_squared.sqrt() + 1e-7)

Adam (RMSProp + Momentum)

moment1 = 0
moment2 = 0
for t in range(num_steps):
    dw = compute_gradient(w)
    moment1 = beta1 * moment1 + (1 - beta1) * dw
    moment2 = beta2* moment2 + (1 - beta2) * dw * dw
    w -= learning_rate * moment1 / (moment2.sqrt() + 1e-7)

这种方式在论文中非常常用，且效果优秀

各个方式的优缺点参照

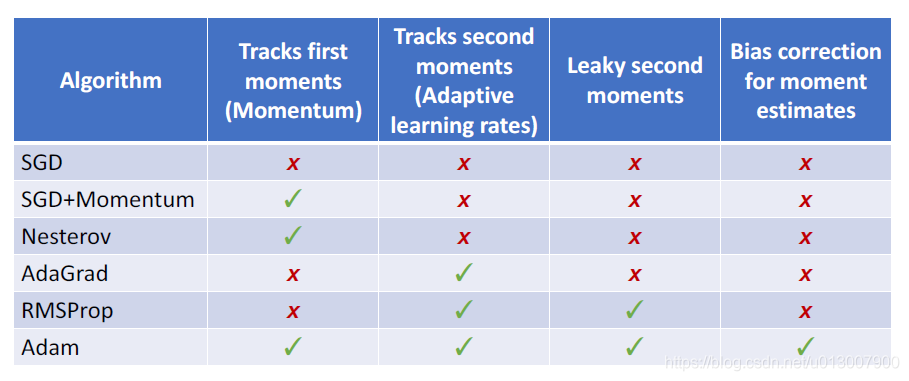
二阶微分

1.使用一阶微分和Hessian矩阵进行二次逼近
2.最小化近似值的步骤

这玩意儿不太行的原因是因为Hessian矩阵有$O(N^2)$个数据，但是N在现实中可能会上百万千万，代价太大。