傅里叶变化的平移性：

 

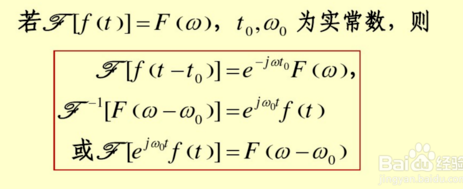
matlab代码验证过程实现：

%% 研究傅里叶变化 的 平移特性
%空间域 乘以exp ，频率域移动

clc;clear
I = imread('rice.jpg');
I  = rgb2gray(I);
I = im2double(I);
figure;subplot(1, 3, 1);imshow(I);title('原图');

%傅里叶变化
f = fft2(I);
f = fftshift(log(1+abs(f)));
subplot(1, 3, 2);imshow(f, []);title('频谱图');

% 图片大小为256*256
% 假设，图像大小为10mm , 那么采样频率为25.6，系统可采集最高频率为25.6/2，
% 每个像素大小为10/256 mm，单位频率是0.1

kx=25.6/2;  %频率。  如果为25.6/2，则移动到最边缘。 为25.6则为一个周期重新回来。
ky=0;  %测试只在x方向（行移动）发生平移
[M,N]=size(I); 
MM=linspace(0,10,256);%1-10 分为256个数，存在MM中。10mm的空间分为256份
NN=linspace(0,10,256);
for i=1:N
     for j=1:M    %MM(i)，NN(j)相当于空间真实坐标
         r(i,j)= exp(1i.*2.*pi.*kx.*MM(i) + 1i.*2.*pi .*ky.*NN(j));  %2pi写在里面了
     end
end
I2= I .* r;
f2 = fft2(I2);
f2 = fftshift(log(1+abs(f2)));
subplot(1, 3, 3);imshow(f2, []);title('平移后-频谱图2');

结果：

中间频率的解释可以参见我的另一篇博客：

除特别声明，本站所有文章均为原创，如需转载请以超级链接形式注明出处：SmartCat's Blog