Slides：百度云 提取码: gs3n

第9课讲的是神经网络的软硬件，感觉比较科普，不做总结。

总览

1. 单次设置
   1. 激活函数
   2. 数据预处理
   3. 权重初始化
   4. 正则化
2. 动态训练
   1. 学习率规划
   2. large-batch 训练；
   3. 超参数优化
3. 训练后
   1. 模型融合
   2. 迁移学习

今天第一讲讲解的是第一点，第二讲将介绍第二点和第三点。

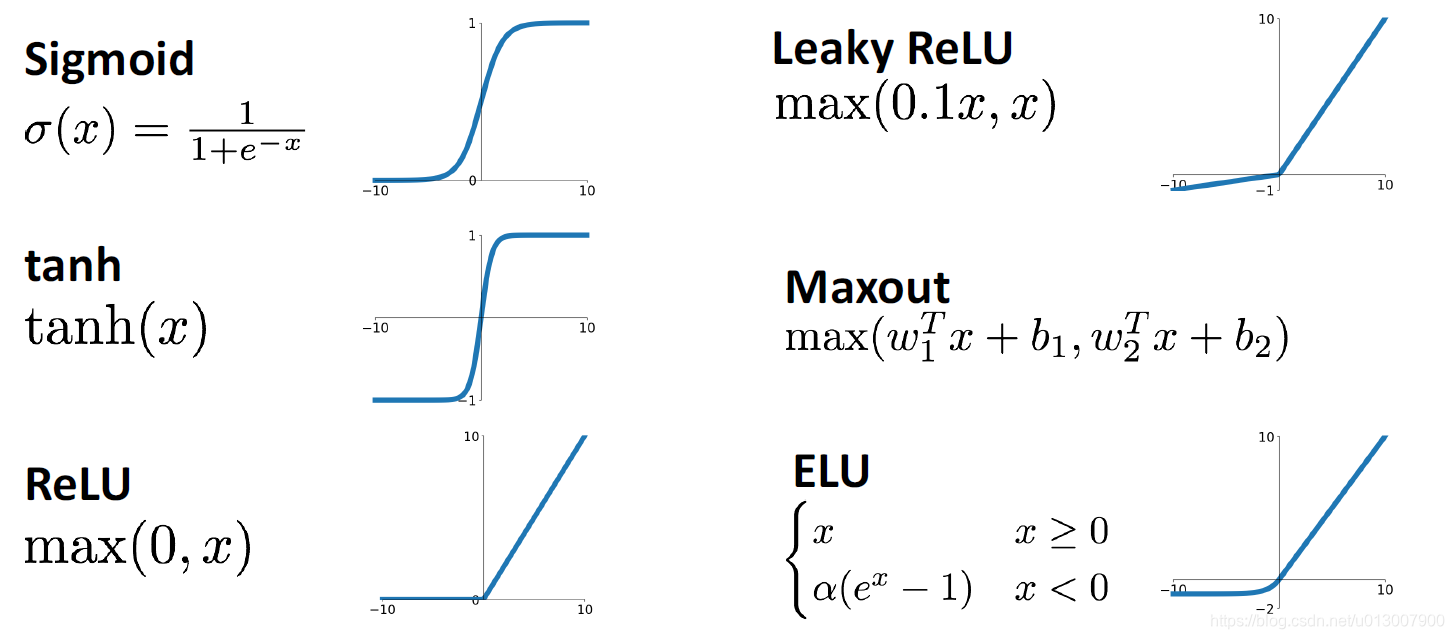
激活函数

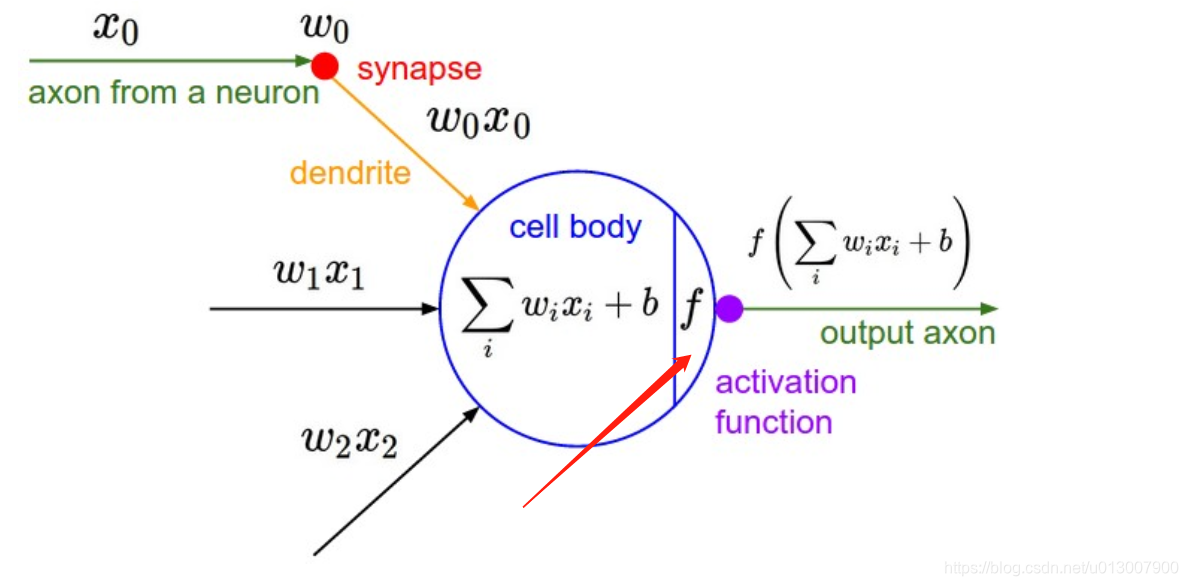
之前也介绍了激活函数是什么，不同的激活函数在训练上，在效果上，在解决问题的方面都各有侧重。下面一一来介绍。

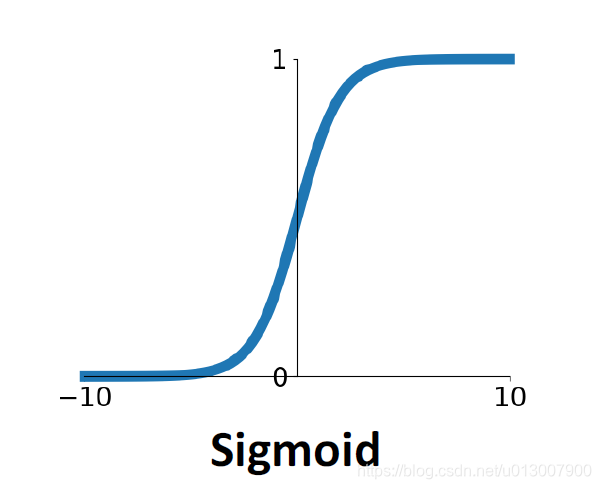
Sigmoid

非常常用的激活函数，在很多线性分类的machine learning模型中也会有用到。

$$\sigma (x)=\frac{1}{1+e^{-x}}$$

• 将函数值限制在[0, 1]之间
• 由于它们可以很好地模拟神经元的饱和“触发率”，因此在历史上很受欢迎
• 通常被用于表示概率，很适合用于表示boolean
• 也是一种非常不错的非线性关系的表达

缺点

• 饱和的神经元将使得梯度下降效果糟糕
  • 我们可以看到在接近$\pm \infty$的时候，梯度是0，这也使得sigmoid难以训练
  • 这种影响甚至会通过链式法则传递到之前的神经元中，导致整个网络的灾难性慢收敛
  • 这是这个函数被弃用的最最最主要原因，其他缺点都是可以接受的
• sigmoid函数的输出中心不是0
  • 在神经元输入全为正的情况下，在计算梯度的时候，w中的每一维都会同为正数。这也导致了训练收敛缓慢。
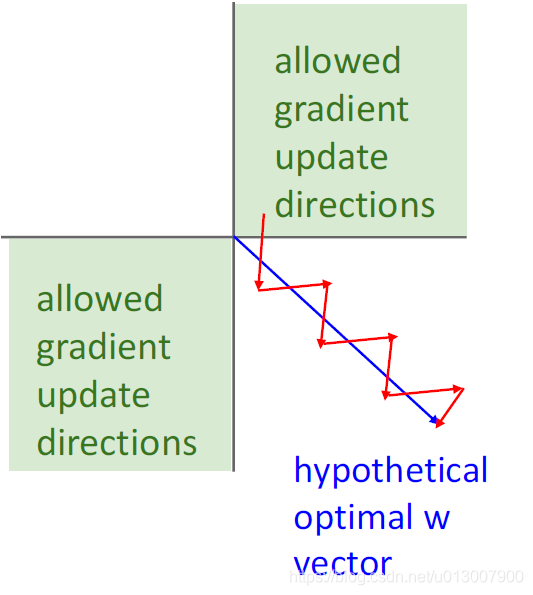  • 虽然在低维处理上面，没什么问题，但是当w是高维的时候，会受到很大的影响。
• Exp()的计算开销大

Tanh

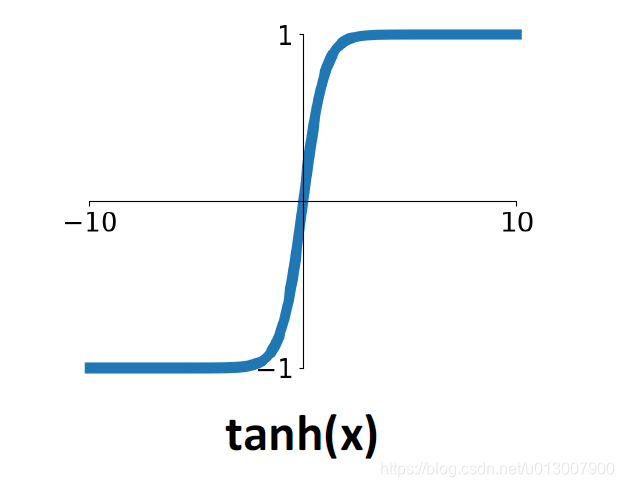
此函数的函数值范围为[-1, 1]，解决了sigmoid函数中心不在0的缺点。

但是还是继承了sigmoid最坏的缺点，在两端的梯度几乎为0.

ReLu

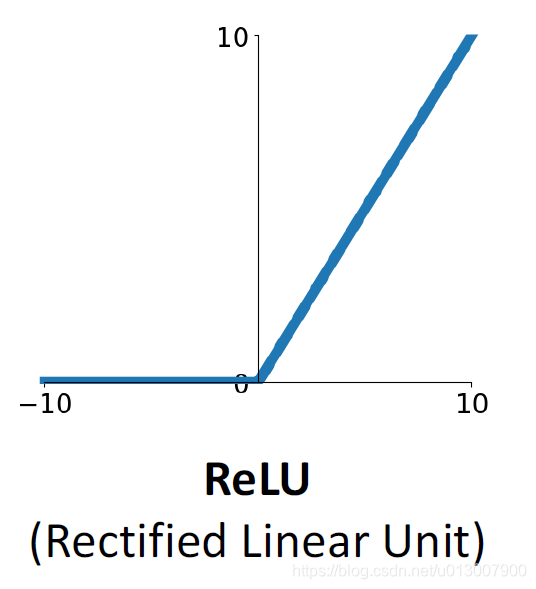
$$f(x)=max(0,x)$$

• 不会在远端让梯度为0
• 计算上非常高效
• 收敛比sigmoid、tanh快多了

缺点

• 不以0为中心

• 当x<0时，梯度的情况令人担忧

  • 甚至情况比sigmoid还糟糕，因为当x<0时，它完全不会收敛。
  • 有时候，我们在初始化ReLu神经元的bias的时候，我们不会设置为0，而是0.01

  Leaky ReLU

  
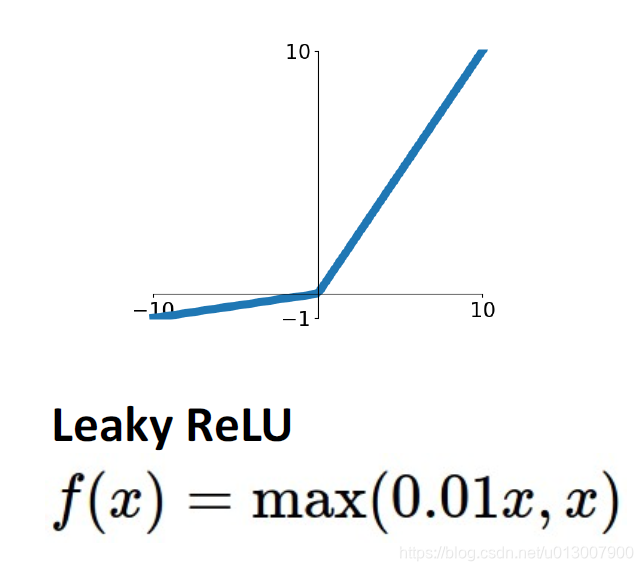
  继承了ReLu的优点，并且在x<0的时候，梯度不会变成0

扩展开后

$$f(x)=max(\alpha x,x)$$

其中$\alpha$是backprop的一个超参数。

Exponential Linear Unit

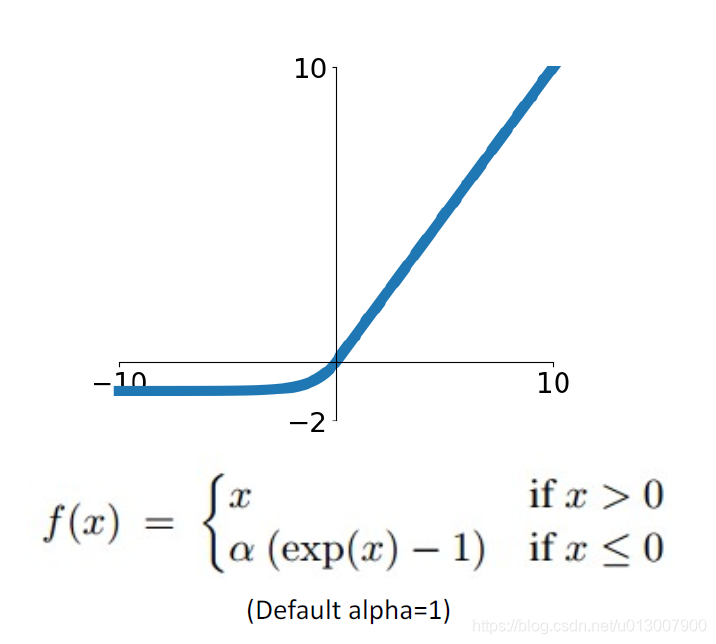
• 继承了ReLu的所有优点
  • 除了Exp()的计算消耗比较大
• 均值输出接近0
  • 这点我有点没明白
• 相比于Leaky ReLu，在x<0的表现，能更加robust，对noise不敏感

Scaled Exponential Linear Unit (SELU)

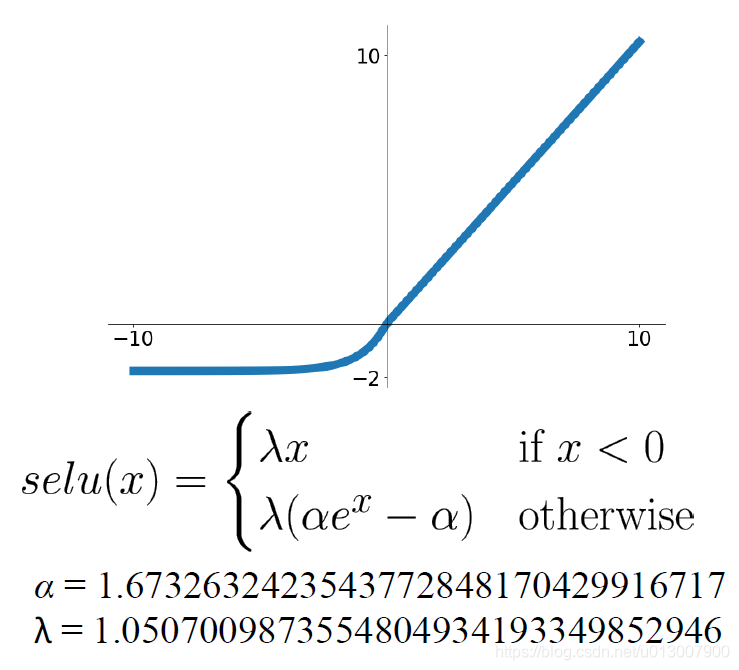
• ELU的扩展版本，在深度网络中表现更好
• 能够自我归一化，使得不需要在训练的时候进行BatchNorm
• 此处给出的$\alpha$和$\lambda$是经过试验测试以及数学论证，得出来效果最好的两个值。

总结

• 无脑使用ReLu，中正平和，不会有太多问题
• 使用ReLu的其他变形，但是基本不会有太多影响，可能是最后0.1%的优化
• 不要使用sigmoid和tanh

PS： 为什么使用的都是单调函数，而不是类似于sin，cos这样的函数，是因为对于一个y，如果存在多个x值，会使得信息有所混乱，导致NN不容易学习特征。

数据预处理

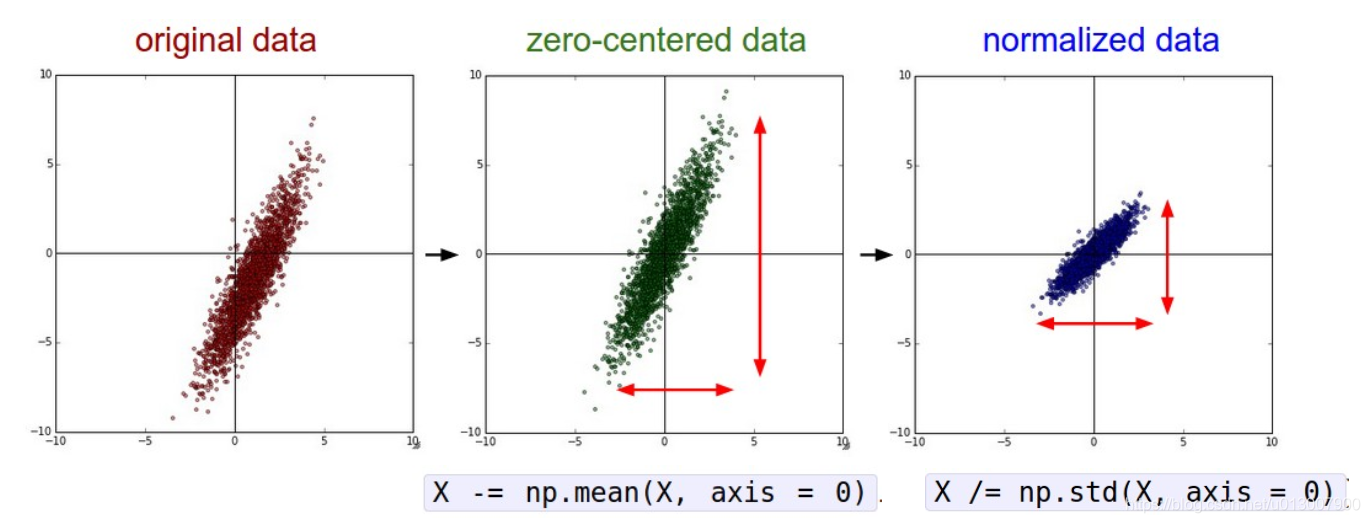
1. 为什么想要将数据中心变成0
   1. 比如，在之前提到的sigmoid中，如果数据集全是正的，或者全是负的，会导致W的gradient的方向是同一个符号的。这个问题就可以通过修正数据集的中心来解决。
2. 归一化的好处。
   1. 降低noise的影响
   2. 将数据缩小到一个合理的范围，使得W更好收敛。

这几个操作，都是在图片识别中相当常用的方式。对于其他种类的问题，都有一些特殊的数据预处理方法。

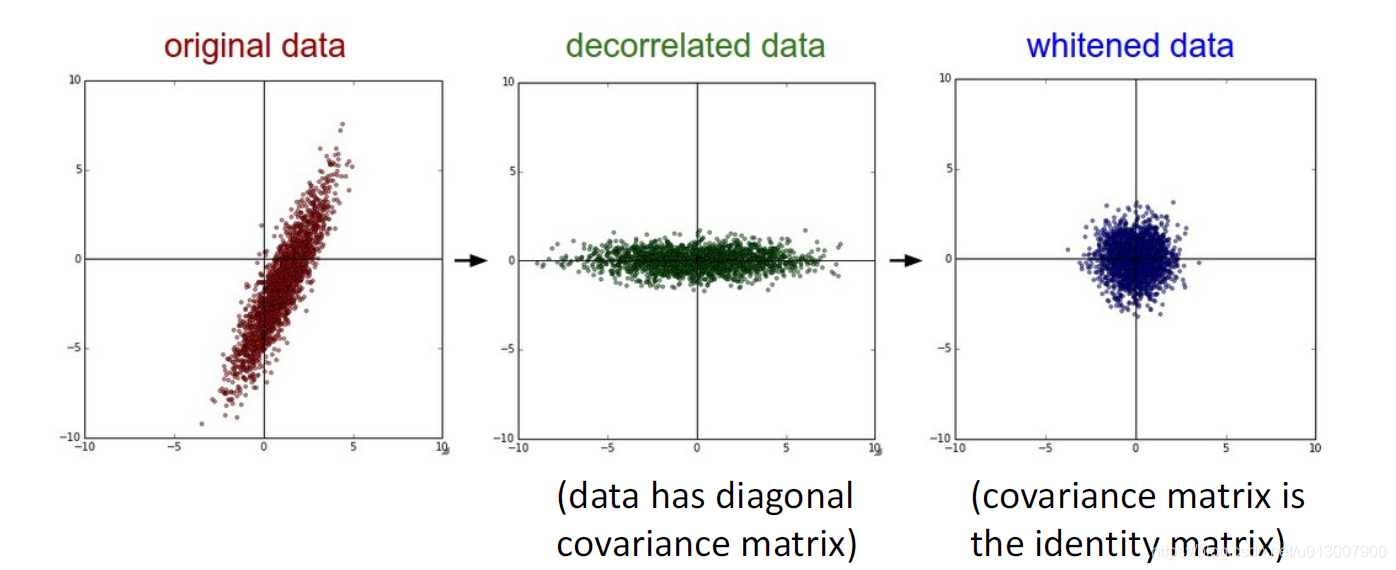
还有接下里两种PCA和whitening。

前者是主成分分析，降维的常用算法。
后者是白化，将数据集的特征之间相关性降低；使得所有特征具有相同的方差。

权重初始化

全0

Q: 如果一个神经网络，将weight和bias全都初始化为0，这是一个好的方式吗？

A：当然不行，这样所有的输出也会是0（假设激活函数是以0为中心的），然后所有的梯度将会是一样。

较小的随机数

用正态分布，中心为0，std=0.01.

W = 0.01 * np.random.randn(Din, Dout)

对于一个小型的神经网络，这是一个非常不错的初始化方法。
对于更深的神经网络，这就不是一个很好的方式了。

问题1

假设有6层神经网络，都用上述方式去初始化W。

我们可以明显感觉到随着层数的增加，因为W的累乘，output也会越来越小。

再考虑考虑梯度的变化。

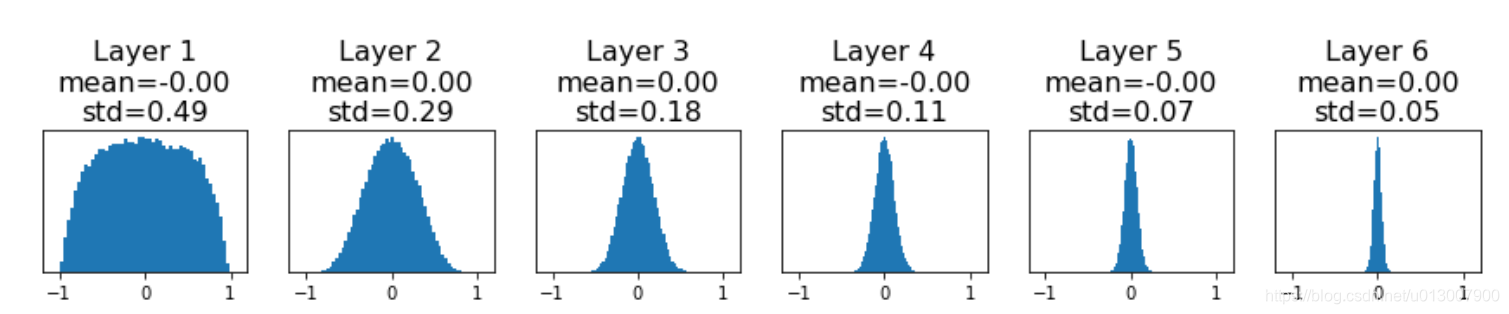
我们可以看到因为W逐渐减小，梯度也越发向0集中。如果一个神经网络非常深，那么结果就是output全是0，没有任何梯度，也没法学习。

问题2

那么我们用一个稍微大一些的std去初始化呢？

比如，std=0.05

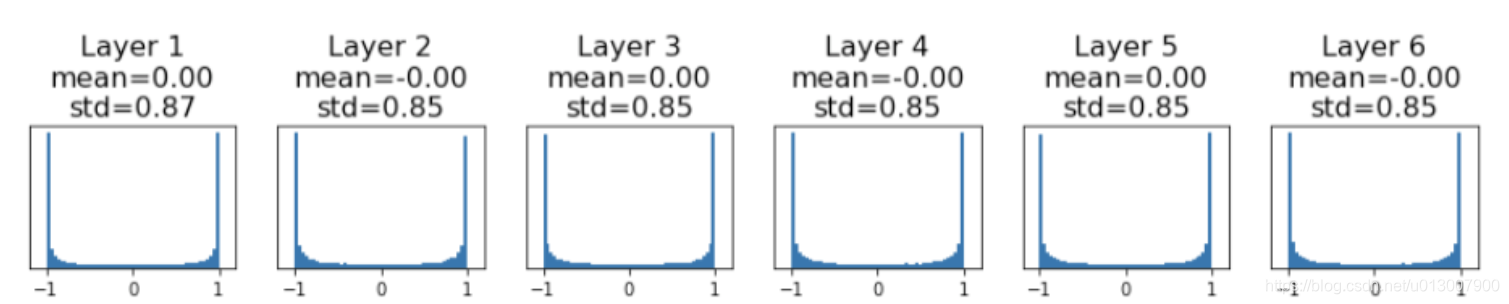
梯度的分布如上
我们可以看到，梯度往-1和1聚集，那么local gradient就会变成0。

Xavier Initialization

将正则分别的std设置为1/sqrt(Din)，从而使得每一个输入输出都能有恰好的大小。

对于卷积层而言，Din是kernel_size ^ 2 * input_channels

原理

这样，输入和输出的方差是一样的

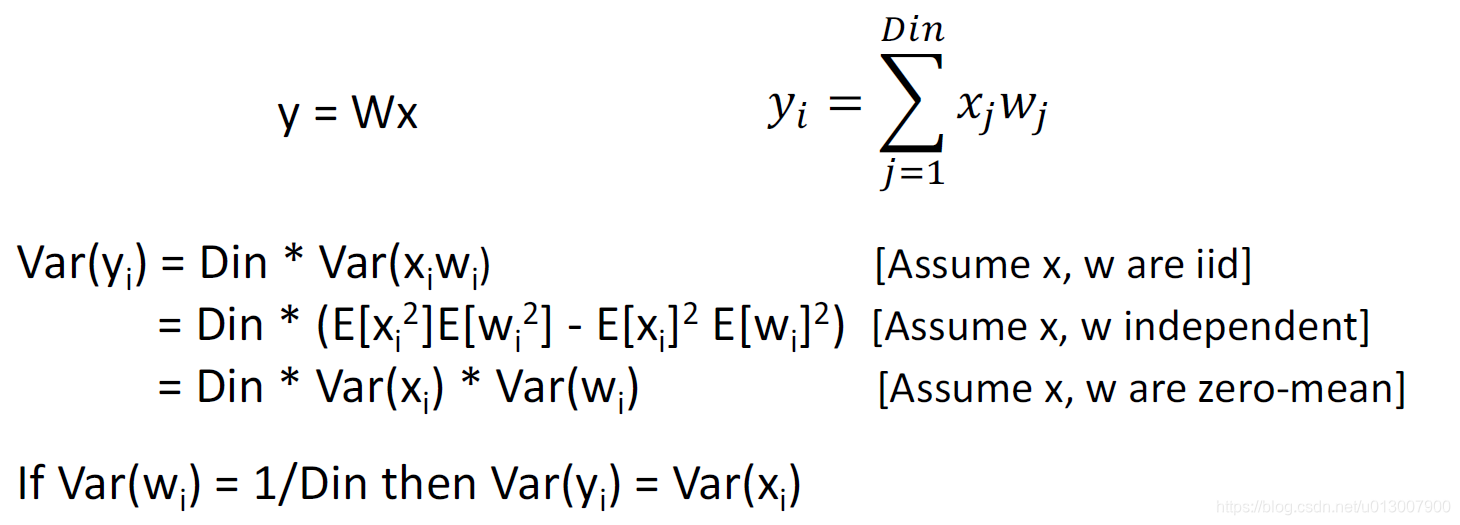
因此保证了gradient分布地均匀

激活函数是ReLu的情况呢？

之前我们都是使用tanh作为激活函数，那么使用ReLu呢？

我们发现，梯度再一次聚集了，他们聚集在0处，再一次使得训练难以进行。

Kaiming / MSRA Initialization

进行修正，std = sqrt(2 / Din)

结果如下

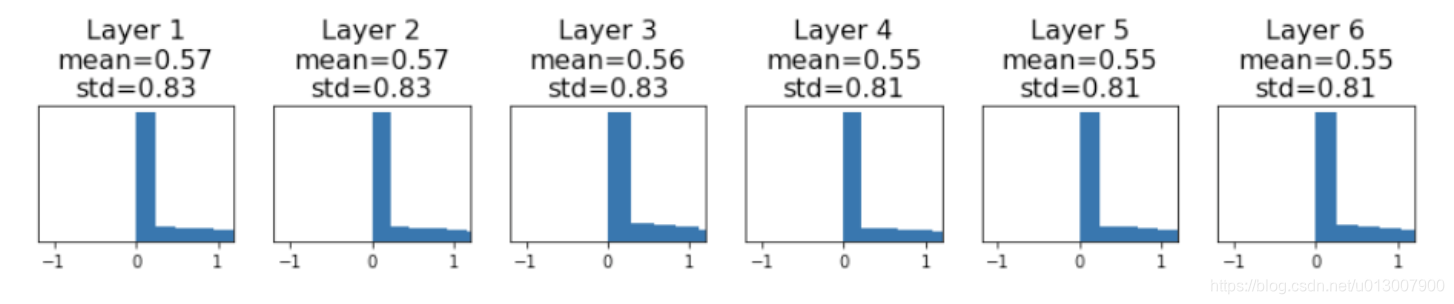
之所以要这么修正，正是我们想要保持输入输出的variance一致。

Residual Networks

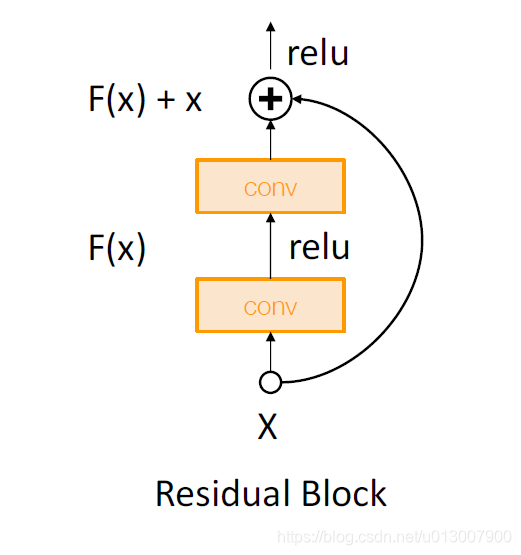
对于这个结构，如果我们使用MSRA，我们能够得出Var(F(x)) = Var(x)。
但是我们的实际输出是Var(F(x)+x) > Var(x)，经过每一个Block，variance都会增长。

解决办法，对第一个conv使用MSRA，对于第二个conv赋值为0.
那么这个时候，Var(F(x)+x) = Var(x)

正则化

其实怎么判断overfit，是一个需要经验的工作。

在Loss函数后面增加一项

常用的几种

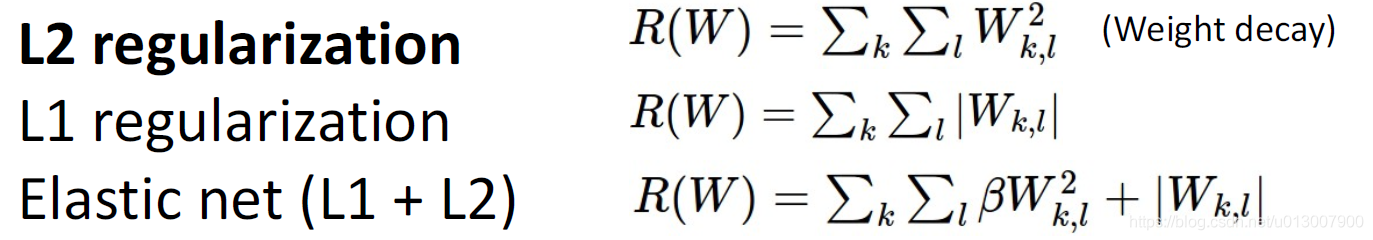
Dropout

在向前传播的过程中，随机将一些神经元的输出设置为0

这个概率是一个超参数，0.5是一个比较常用的

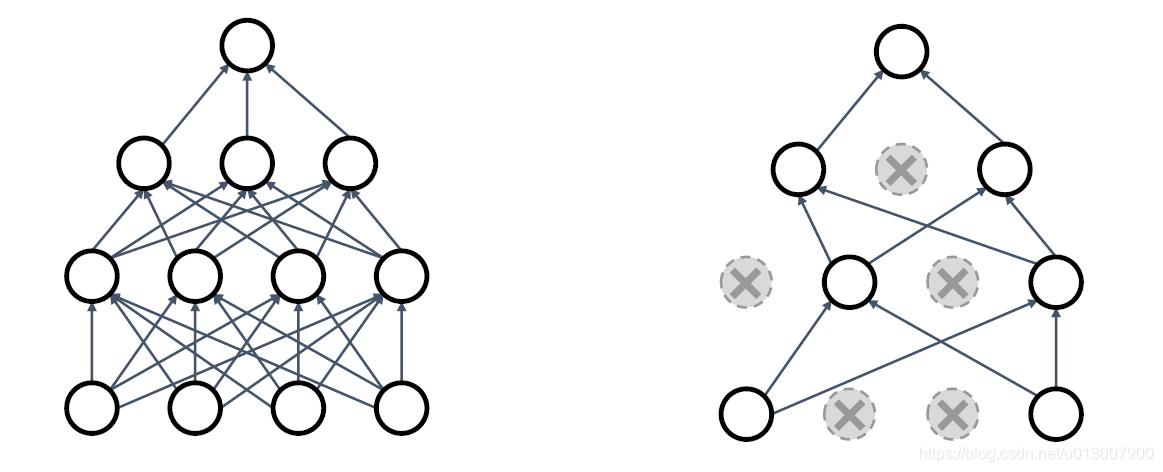
dropout的作用是

1. 强制网络具有冗余表示形式
   1. 即，舍弃了一部分神经元也能提取出相似的特征
2. 防止特征的共适性
   1.即，两个特征不一定要一同出现才能让机器做出判断

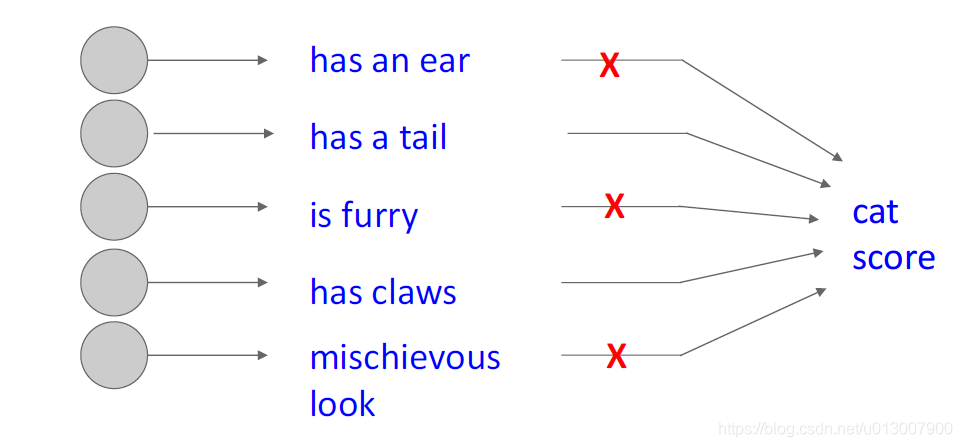
另一种解释

Dropout是一种多模型（共享参数）的融合。
每一个二元的取舍都是一个新的模型。

对于一个4096个单元的全连接层，会有$2^{4096}$ ~$10^{1233}$种可能性

测试中的dropout

随机将输出舍弃

这并不是一个明智的决定。

因为我们可以用数据公式论证一下，这样的行为和在training中的dropout产生的输出期望，并不一样。

这种东西，复杂且难以估量。并不是一个理论上非常优秀的结果。

输出乘以dropout概率

测试的时候
$$E[a]=w_{1}x+w_{2}y$$
训练的时候

我们发现，在测试的时候，并不需要dropout
我们只需要在输出的时候，乘以dropout的概率，即可

DropConnect

和一般的Dropout不同的是，它是，神经元之间的连接是随机的

这样在测试的时候，我们只需要将所有的东西连上即可。

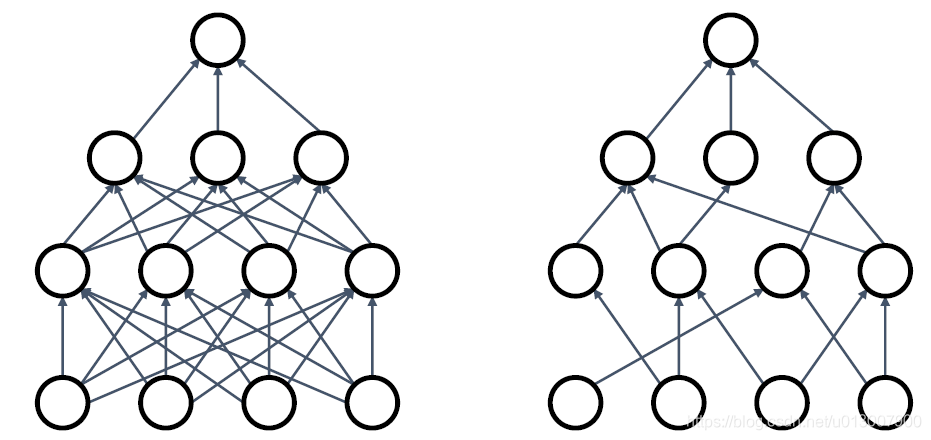
Fractional Pooling

使用随机的pooling区域。

测试的时候，取各个sample size pooling结果的平均值

Stochastic Depth

随机跳过一些ResBlock

测试的时候，使用全网络

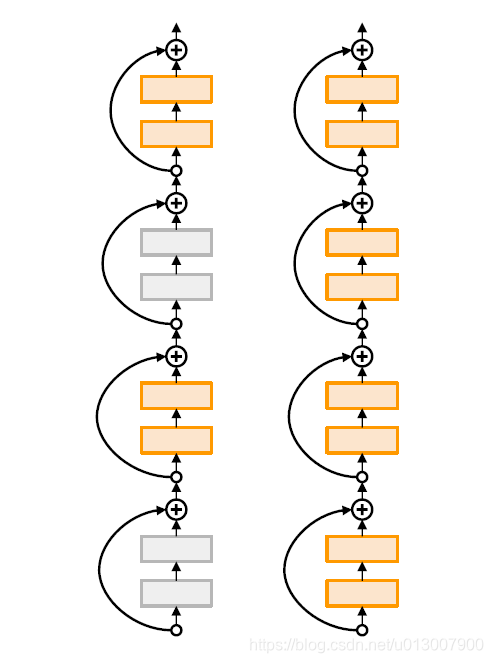
Stochastic Depth

遮盖（随机将一部分像素设置为0）

在小的数据集上表现优秀，在大的数据集上更加少见。

混合

数据扩充

通常而言，训练集肯定是越多越好，但是有时候训练集并不是很足够，我们就需要一些别的方式来扩充数据。

这是我之前写的博文的例子，

除特别声明，本站所有文章均为原创，如需转载请以超级链接形式注明出处：SmartCat's Blog