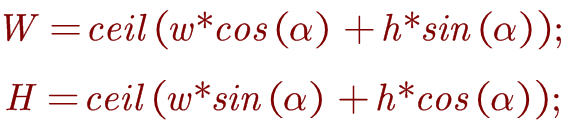Matlab:图像平移算法的原理实现，缺陷分析及优化

1.怎么样确定平移之后新的图片的模板呢?

这里，我们主要通过转换公式来实现：

W，H代表平移后的图片模块大小；而ceil()代表上取整，w，h代表原来图片的大小，Apha为旋转角度。经代码实现后，我们可以得到新的图片模板：

img=imread('pet.jpg');
subplot(2,2,1),imshow(img);
[h,w,k]=size(img);
a=80;
a=a*pi/180;
w_new=ceil(w*cos(a)+h*sin(a));
h_new=ceil(w*sin(a)+h*cos(a));
img_new=zeros(h_new,w_new,k);
%旋转
subplot(2,2,2),imshow(img_new);

如图所示：

2.图像中的坐标平移转换是如何实现的呢？

在实现平移算法之前，我们首先来了解平移算法的背景知识：

以逆时针旋转为例：

如图，旋转前的坐标为：

$x_0=rcos\theta$
$y_0=r\sin \theta$
而旋转后的坐标为：
${\chi }_1:$
$=rcos\left(\theta +\alpha \right)$
$=rcos\theta cos\alpha -rsin\theta sin\alpha$
$=x_{0}cos\alpha -y_{0}sin\alpha$
$y_1:$
$=rsin\left(\theta +\alpha \right)$
$=r\sin \theta cos\alpha +r\cos \theta sin\alpha$
$=x_0\sin \alpha +y_0\cos \alpha$

通过以上的计算，我们可以得到平移矩阵：

这个时候，如果你对图像处理有一定的了解的话，你会发现这里的坐标采用的是数学里面的笛卡尔坐标系，而并不是我们的图像的坐标系。所以，为了实现坐标的转换，我们首先得实现坐标系的统一。

那么我们如何将图像坐标系转换为笛卡尔坐标系（也就是我们熟悉的数学坐标系）呢?

坐标系平移：

设图像宽度为W，高度为H，通过坐标系原点之间的位置关系，我们不难发现，由坐标系Ⅰ平移到Ⅱ的变换矩阵为：

而其逆矩阵为：

而我们得到图像平移的设计思路如下:

• 将像素所在的图像坐标系转换为笛卡尔坐标系。
• 将笛卡尔坐标系下的像素进行平移变换。
• 将像素所在的笛卡尔坐标系转换为图像坐标系。

coordination_shift=[1 0 -0.5*w;0 -1 0.5*h;0 0 1];%坐标系转换转换矩阵
rotation=[cos(a) -sin(a) 0; sin(a) cos(a) 0;0 0 1];%旋转矩阵
shift_back=[1 0 0.5*w_new;0 -1 0.5*h_new; 0 0 1];%还原坐标系矩阵

for y=1:h
    for x=1:w
        xy_position=coordination_shift*[x;y;1];%将像素所在的图像坐标系转换为笛卡尔坐标系。
        xy_rotation=rotation*xy_position;%将笛卡尔坐标系下的像素进行平移变换。
        xy_new=round(shift_back*xy_rotation);%将像素所在的笛卡尔坐标系转换为图像坐标系。
        img_new(xy_new(2),xy_new(1),:)=img(y,x,:);
        end
    end
end
subplot(2,2,3),imshow(uint8(img_new));

通过如上的算法及代码实现，我们可以得到基于图像平移算法的实现操作。

3.上述步骤实现的图像平移算法的缺陷及优化

问题一，当旋转角度过大时，无法实现图像平移?

原因分析：

当角度过大时，图像的像素位置经过笛卡尔坐标系下的旋转后，还原为图像坐标系后可能会发生越界情况，导致无法实现其平移。

解决方法：

当经过旋转后还原为图像坐标系的像素点发生越界情况后，舍弃这些像素点:

 xy_new=round(shift_back*xy_rotation);%将像素所在的笛卡尔坐标系转换为图像坐标系。
   if xy_new(2)>0&&xy_new(2)<h+1&&xy_new(1)>0&&xy_new(1)<w+1
            img_new(xy_new(2),xy_new(1),:)=img(y,x,:);

问题二，经过平移后的图像内部会存在大量黑点?

原因分析：

因为旋转的计算采用了sin(),cos()三角函数计算，经过ceil()变化后，像素点会存在精度上的缺失。

解决方法：

这里，我采用的是当像素缺失点(x,y)的“四领域”均存在像素值时，该点填充像素点(x+1,y)的像素值。

for y=2:h_new-1
    for x=2:w_new-1%这里需要注意的是，防止越界。
       if img_new(y,x,:)==0
               img_new(y,x,:)=padding(x,y,img_new);
       end
    end
end
subplot(2,2,4),imshow(uint8(img_new));

%自定义判定函数
function [result]=padding(x,y,img)
result=0;
if img(y-1,x,:)>0
    if img(y,x-1,:)>0
        if img(y+1,x,:)>0
            if img(y,x+1,:)>0
                result=img(y,x+1,:);
            else
                result=0;
            end
        end
    end
end
end

效果展示：

问题三，如何更好地优化填充算法呢？

其实经过上述的填充算法，当旋转角度小于90°时，填充的效果较好；当旋转角度大于90时，如何更好地优化填充算法呢?这是留给笔者和阅读这篇文章的读者值得思考的问题。(｡◕ˇ∀ˇ◕)